K-means clustering: problem

• Data

  • \(D\)-dimensional observations: \(\mathbf{x}_1, \ldots, \mathbf{x}_N\)

• Parameters

  • \(K\) clusters’ means: \(\boldsymbol\mu_1, \ldots, \boldsymbol\mu_K\)
  • Binary indicator \(r_{nk} \in \{0, 1\}\): if object \(n\) is in class \(k\)

• Goal: find values for \(\{\boldsymbol\mu_k\}\) and \(\{r_{nk}\}\) to minimize the objective function (called a distortion measure) \[ J = \sum_{n=1}^N \sum_{k = 1}^K r_{nk} \|\mathbf{x}_n - \boldsymbol\mu_k \|^2 \]

K-means clustering: solution

• Two-stage optimization

  • Update \(r_{nk}\) and \(\boldsymbol\mu_k\) alternatively, and repeat until convergence
  • Resembles the E step and M step in the EM algorithm

1. E(expectation) step: updates \(r_{nk}\).

   • Assign the \(n\)th data point to the closest cluster center \[ r_{nk} = \begin{cases} 1 & \text{ if } k = \arg\min_j \|\mathbf{x}_n - \boldsymbol\mu_k \|^2\\ 0 & \text{ otherwise} \end{cases} \]

2. M(maximization) step: updates \(\boldsymbol\mu_k\)

   • Set cluster mean to be mean of all data points assigned to this cluster \[ \boldsymbol\mu_k = \frac{\sum_{n} r_{nk} \mathbf{x}_n}{\sum_{n} r_{nk}} \]

Mixture of Gaussians: definition

• Mixture of Gaussians: log likelihood \[\begin{equation}\label{eq:mixture_of_gaussians} \log p(\mathbf{x}) = \log \left\{ \sum_{k = 1}^K \pi_k \cdot \text{N}\left(\mathbf{x} \mid \boldsymbol\mu_k, \boldsymbol\Sigma_k \right) \right\} \end{equation}\]

• Introduce a \(K\)-dim latent indicator variable \(\mathbf{z}\in \{0, 1\}^K\) \[ z_k = \mathbf{1}(\text{if $\mathbf{x}$ is from the $k$-th Gaussian component}) \]

The marginal distribution of \(\mathbf{z}\) is multinomial \[ p(z_k = 1) = \pi_k \]

• We call the posterior probability as the Responsibility that component \(k\) takes for explaining the observation \(\mathbf{x}\) \[ \gamma(z_k) = p(z_k = 1\mid \mathbf{x}) = \frac{\pi_k \cdot \text{N}\left(\mathbf{x} \mid \boldsymbol\mu_k, \boldsymbol\Sigma_k \right)} {\sum_{j=1}^K \pi_j \cdot \text{N}\left(\mathbf{x} \mid \boldsymbol\mu_j, \boldsymbol\Sigma_j \right)} \]

Mixture of Gaussians: singularity problem with MLE

• Problem with maximum likelihood estimation: presence of singularities: there will be clusters that contains only one data point, so that the corresponding covariance matrix will be estimated at zero, thus the likelihood explodes

  • Therefore, when finding MLE, we should avoid finding such singularity solution and instead seek well-behaved local maxima of the likelihood function: see the following EM approach

  • Alternatively, we can to adopt a Bayesian approach

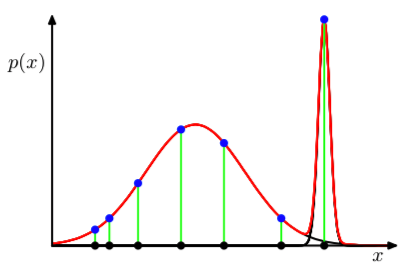
Figure 1: Illustration of singularities

Conditional MLE of \(\boldsymbol\mu_k\)

• Suppose we observe \(N\) data points \(\mathbf{X} = \{\mathbf{x}_1, \ldots, \mathbf{x}_N\}\)

• Similarly, we write the \(N\) latent variables as \(\mathbf{Z} = \{\mathbf{z}_1, \ldots, \mathbf{z}_N\}\)

• Set the derivatives of \(\log p(\mathbf{X} \mid \boldsymbol\pi, \boldsymbol\mu, \boldsymbol\Sigma)\) with respect to \(\boldsymbol\mu\) to zero \[ 0 = \sum_{n=1}^N \gamma(z_{nk}) ~\boldsymbol\Sigma_k ~\left(\mathbf{x}_n - \boldsymbol\mu_k \right) \] Then we obtain \[ \boldsymbol\mu_k = \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk})~ \mathbf{x}_n \] where \(N_k\) is the effective number of points assigned to cluster \(k\) \[ N_k = \sum_{n=1}^N \gamma(z_{nk}) \]

Conditional MLE of \(\boldsymbol\Sigma_k\) and \(\pi_k\)

• Similarly, setting the derivatives of log likelihood wrt \(\boldsymbol\Sigma_k\), we have \[ \boldsymbol\Sigma_k = \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk})~ \left(\mathbf{x}_n - \boldsymbol\mu_k\right)\left(\mathbf{x}_n - \boldsymbol\mu_k\right)^\top \]

• Use Lagrange multiplier to maximize log likelihood wrt \(\pi_k\) under the constraint that all \(\pi_k\) add up to one: \[ \log p(\mathbf{X} \mid \boldsymbol\pi, \boldsymbol\mu, \boldsymbol\Sigma) + \lambda \left( \sum_{k=1}^K \pi_k - 1 \right) \] we get the solution \[ \pi_k = \frac{N_k}{N} \]

• The above results on \(\boldsymbol\mu_k, \boldsymbol\Sigma_k, \pi_k\) are not closed-form solution because the responsibilities \(\gamma(z_{nk})\) depend on them in a complex way.

EM algorithm for mixture of Gaussians

1. Initialize \(\boldsymbol\mu_k, \boldsymbol\Sigma_k, \pi_k\), usually using the \(K\)-means algorithm.

2. E step: compute responsibilities using the current parameters \[ \gamma(z_{nk}) = \frac{\pi_k \cdot \text{N}\left(\mathbf{x}_n \mid \boldsymbol\mu_k, \boldsymbol\Sigma_k \right)} {\sum_{j=1}^K \pi_j \cdot \text{N}\left(\mathbf{x}_n \mid \boldsymbol\mu_j, \boldsymbol\Sigma_j \right)} \]

3. M step: re-estimate the parameters using the current responsibilities, where \(N_k = \sum_{n=1}^N \gamma(z_{nk})\) \[\begin{align*} \boldsymbol\mu_k^{\text{new}} & = \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk})~ \mathbf{x}_n\\ \boldsymbol\Sigma_k^{\text{new}} & = \frac{1}{N_k} \sum_{n=1}^N \gamma(z_{nk})~ \left(\mathbf{x}_n - \boldsymbol\mu_k\right)\left(\mathbf{x}_n - \boldsymbol\mu_k\right)^\top\\ \pi_k^{\text{new}} & = \frac{N_k}{N} \end{align*}\]

4. Check for convergence of either the parameters or the log likelihood. If not converged, return to step 2.

Connection between K-means and Gaussian mixture model

• K-means algorithm itself is often used to initialize the parameters in a Gaussian mixture model before applying the EM algorithm

• Mixture of Gaussians: soft assignment of data points to clusters, using posterior probabilities

• \(K\)-means can be viewed as a special case of mixture of Gaussian, where covariances of mixture components are \(\epsilon \mathbf{I}\), where \(\epsilon\) is a parameter shared by all components.

  • In the responsibility calculation, \[ \gamma(z_{nk}) = \frac{\pi_k \exp\{-\| \mathbf{x}_n - \boldsymbol\mu_k\|^2 / 2\epsilon \}} {\sum_j \pi_j \exp\{-\| \mathbf{x}_n - \boldsymbol\mu_j\|^2 / 2\epsilon \}} \] In the limit \(\epsilon\rightarrow 0\), for each observation \(n\), the responsibilities \(\{\gamma(z_{nk}), k = 1, \ldots, K\}\) has exactly one unity and all the rest are zero.

EM algorithm: definition

• Goal: maximize likelihood \(p(\mathbf{X} \mid \boldsymbol\theta)\) with respect to the parameter \(\boldsymbol\theta\), for models having latent variables \(\mathbf{Z}\).

• Notations
  • \(\mathbf{X}\): observed data; also called incomplete data
  • \(\boldsymbol\theta\): model parameters
  • \(\mathbf{Z}\): latent variables, usually each observation has a latent variable
  • \(\{\mathbf{X}, \mathbf{Z}\}\) is called complete data
• Log likelihood \[ \log~p(\mathbf{X} \mid \boldsymbol\theta) = \log\left\{ \sum_{\mathbf{Z}} p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta) \right\} \]
  • The sum over \(\mathbf{Z}\) can be replaced by an integral if \(\mathbf{Z}\) is continuous
  • The presence of sum prevents the logarithm from acting directly on the joint distribution. This complicates MLE solutions, especially for exponential family.

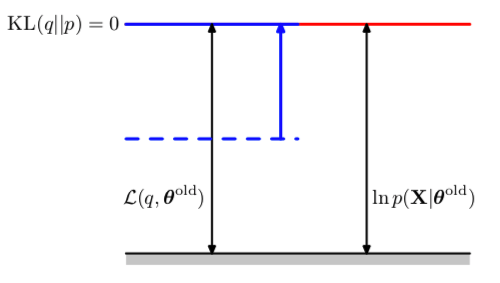
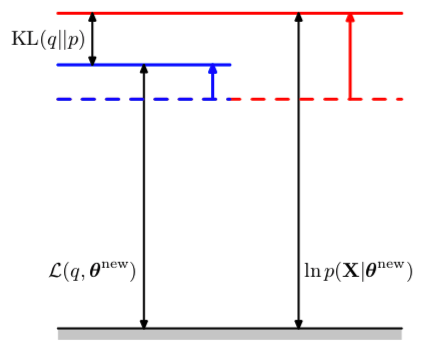
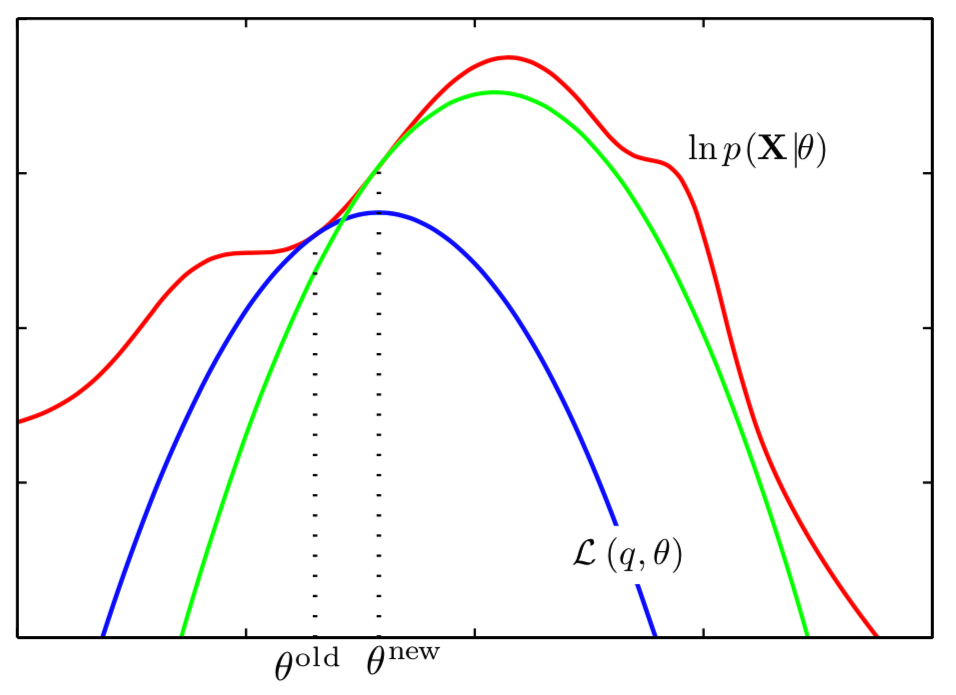
General EM algorithm: two-stage iterative optimization

1. Choose the initial parameters \(\boldsymbol\theta^{\text{old}}\)

2. E step: since the conditional posterior \(p\left( \mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}} \right)\) contains all of our knowledge about the latent variable \(\mathbf{Z}\), we compute the expected complete-data log likelihood under it. \[\begin{align*} \mathcal{Q}(\boldsymbol\theta, \boldsymbol\theta^{\text{old}}) & = E_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}}} \left\{\log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta) \right\} \\ & = \sum_{\mathbf{Z}} p\left( \mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}} \right) \log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta) \end{align*}\]

3. M step: revise parameter estimate \[ \boldsymbol\theta^{\text{new}} = \arg\max_{\boldsymbol\theta} \mathcal{Q}(\boldsymbol\theta, \boldsymbol\theta^{\text{old}}) \]
   • Note in the maximizing step, the logarithm acts driectly on the joint likelihood \(p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta)\), so the maximizating will be tractable.

4. Check for convergence of the log likelihood or the parameter values. If not converged, use \(\boldsymbol\theta^{\text{new}}\) to replace \(\boldsymbol\theta^{\text{old}}\), and return to step 2.

Gaussian mixtures revisited

• Recall that latent variables \(\mathbf{Z}\in \mathbb{R}^{N \times K}\) : \[ z_{nk} = \mathbf{1}(\text{if $\mathbf{x}_n$ is from the $k$-th Gaussian component}) \]
• Complete data log likelihood \[ \log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\mu, \boldsymbol\Sigma, \boldsymbol\pi) = \sum_{n=1}^N \sum_{k=1}^K z_{nk}\left\{\log \pi_k + \log \text{N}\left(\mathbf{x}_n \mid \boldsymbol\mu_k, \boldsymbol\Sigma_k \right) \right\} \]
  • Comparing this with incomplete data log likelihood in Eq , we have the sum over \(k\) and logarithm interchanged. Thus, the logarithm acts on Gaussian density directly.

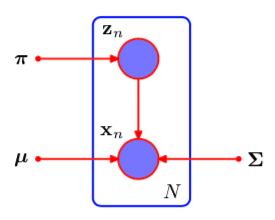
Figure 2: Mixture of Gaussians, treating latent variables as observed

Continue: Gaussian mixtures revisited

• Conditional posterior of \(\mathbf{Z}\) \[ p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol\mu, \boldsymbol\Sigma, \boldsymbol\pi) \propto \prod_{n=1}^N \prod_{k=1}^K \left[\pi_k \text{N}\left(\mathbf{x}_n \mid \boldsymbol\mu_k, \boldsymbol\Sigma_k \right) \right]^{z_{nk}} \] Thus, the conditional posterior of \(\{\mathbf{z}_n\}\) are independent

• Conditional expectations \[ E_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol\mu^{\text{old}}, \boldsymbol\Sigma^{\text{old}}, \boldsymbol\pi^{\text{old}}}~z_{nk} = \gamma(z_{nk})^{\text{old}} \]

• Thus the objective function in the M-step \[\begin{align*} & E_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol\mu^{\text{old}}, \boldsymbol\Sigma^{\text{old}}, \boldsymbol\pi^{\text{old}}}~ \log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\mu, \boldsymbol\Sigma, \boldsymbol\pi)\\ = & \sum_{n=1}^N \sum_{k=1}^K \gamma(z_{nk})^{\text{old}}\left\{\log \pi_k + \log \text{N}\left(\mathbf{x}_n \mid \boldsymbol\mu_k, \boldsymbol\Sigma_k \right) \right\} \end{align*}\]

A different view of the EM algorithm

• Goal: maximize the incomplete data likelihood \[ p(\mathbf{X} \mid \boldsymbol\theta) = \sum_{\mathbf{Z}} p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta) \]

• Suppose that optimization of \(p(\mathbf{X} \mid \boldsymbol\theta)\) is difficult, but optimization of \(p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta)\) is significantly easier.

• An important decompsition: holds for any arbitrary distribution \(q(\mathbf{Z})\) \[\begin{equation}\label{eq:em_decomposition} \log p(\mathbf{X} \mid \boldsymbol\theta) = \mathcal{L}(q, \boldsymbol\theta) + \text{KL}(q ~\| ~p) \end{equation}\] where \(\mathcal{L}(q, \boldsymbol\theta)\) is called a lower bound on \(\log p(\mathbf{X} \mid \boldsymbol\theta)\): \[\begin{align*} \mathcal{L}(q, \boldsymbol\theta) & = \sum_{\mathbf{Z}} q(\mathbf{Z}) \log\left\{ \frac{p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta)}{q(\mathbf{Z})} \right\}\\ \text{KL}(q ~\| ~p) & = - \sum_{\mathbf{Z}} q(\mathbf{Z}) \log\left\{ \frac{p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta)}{q(\mathbf{Z})} \right\} \end{align*}\]

  • Note: this formula will appear again in variational inference.

A different view of the EM algorithm: E step

• In E step, the lower bound \(\mathcal{L}(q, \boldsymbol\theta^{\text{old}})\) is maximized with respect to \(q(\mathbf{Z})\) while keeping \(\boldsymbol\theta^{\text{old}}\) fixed

• The solution is when the KL divergence \(\text{KL}\left(q(\mathbf{Z}) ~\|~ p\left(\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}}\right) \right)\) is zero, i.e., \[ q(\mathbf{Z}) = p\left(\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}}\right) \]

Figure 3: In the E step, the lower bound moves to the same value as the old incomplete data log likelihood

A different view of the EM algorithm: M step

• In M step, the distribution \(q(\mathbf{Z})\) is held fixed and the lower bound \(\mathcal{L}(q, \boldsymbol\theta^{\text{old}})\) is maximized wrt \(\boldsymbol\theta\) to give some new value \(\boldsymbol\theta^{\text{new}}\). Thus, the lower bound increases.

• Since \(q(\mathbf{Z})\) is fixed at \(\boldsymbol\theta^{\text{old}}\), it will not equal the new posterior \(p\left(\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{new}}\right)\). Therefore, the KL divergence becomes nonzero.

Figure 4: In the M step, both the lower bound and the KL divergence increase.

EM algorithm illustration

• Red curve: incomplete data log likelihood
• Blue curve: lower bound \(\mathcal{L}(\boldsymbol\theta, \boldsymbol\theta^{\text{old}})\)
• Green curve: lower bound \(\mathcal{L}(\boldsymbol\theta, \boldsymbol\theta^{\text{new}})\)
• The lower bounds have tangential contacts with the log likelihood

Figure 5: Illustration of EM algorithm, in the parameter space

EM algorithm in Bayesian statistics

• EM algorithm can be used to estimate maximum posterior (MAP)

• In this case, the objective function is \[ p(\boldsymbol\theta \mid \mathbf{X}) \propto p(\mathbf{X} \mid \boldsymbol\theta) ~ p(\boldsymbol\theta) \] Hence, the expectation in Step 2 becomes \[\begin{align*} \mathcal{Q}(\boldsymbol\theta, \boldsymbol\theta^{\text{old}}) & = E_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}}} \left\{\log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta) + \log p(\boldsymbol\theta) \right\} \\ & = E_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta^{\text{old}}} \left\{\log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol\theta)\right\} + \log p(\boldsymbol\theta) \end{align*}\]

EM algorithm and missing data

• The latent variables can be the missing values in the data
• This is valid is the data are missing at random

EM algorithm for IID data with \(N\) latent variables

• Suppose \(N\) data points \(\{\mathbf{x}_1, \ldots, \mathbf{x}_N\}\) are IID

• Each observation \(\mathbf{x}_n\) has its corresponding latent variable \(\mathbf{z}_n\)

• Then the conditional posterior of \(\mathbf{Z}\) also factorizes wrt \(n\): \[ p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol\theta) = \prod_{n=1}^N p(\mathbf{z}_n \mid \mathbf{x}_n, \boldsymbol\theta) \]

• Exploit this structure: using incremental form of EM that at each cycle only process one data point
  • Benefit: no need to wait for the whole data set to finish processing

Extensions of EM algorithms

• For complex models, E step and/or M step can be intractable

• Generalized EM (GEM): address an intractable M step
  • Instead of maximizing the objective function in the M step, just changing the parameter to increase its value
  • E.g., using nonlinear optimization methods such as conjugate gradients algorithm
  • E.g., expected conditional maximization (ECM), constrained optimization

• We can also generalize the E step: find \(q(\mathbf{Z})\) to partially, rather than completely, optimize \(\mathcal{L}(q, \boldsymbol\theta)\)

References

• Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.