For the pdf slides, click here
Notations
In this chapter, we assume that there is only one variable having missing values. We call this variable the target variable.
- : the observed data in
- : the missing data in
- : imputed values in
Suppose are the variables (covariates) in the imputation model.
- : the subset of rows of which is observed
- : the subset of rows of which is missing
Imputation under the Normal Linear Model
Four methods to impute under the normal linear model
- Regression imputation: Predict (bad!). Fit a linear model on the observed data and get the OLS
estimates . Impute with the predicted values
- In
micepackage, this method isnorm.predict
- In
- Stochastic regression imputation: Predict + noise (better, but still bad). Also add a random drawn noise
from the estimated residual normal distribution
- In
micepackage, this method isnorm.nob
- In
Method 3: Bayesian multiple imputation
Predict + noise + parameter uncertainty
Under the priors (where the hyper-parameter is fixed at a small value, e.g., ) We draw (including both and ), from the posterior distribution
In
micepackage, this method isnorm
Method 4: Bootstrap multiple imputation
Predict + noise + parameter uncertainty where , , and are OLS estimates calculated form a bootstrap sample taken from the observed data
In
micepackage, this method isnorm.boot
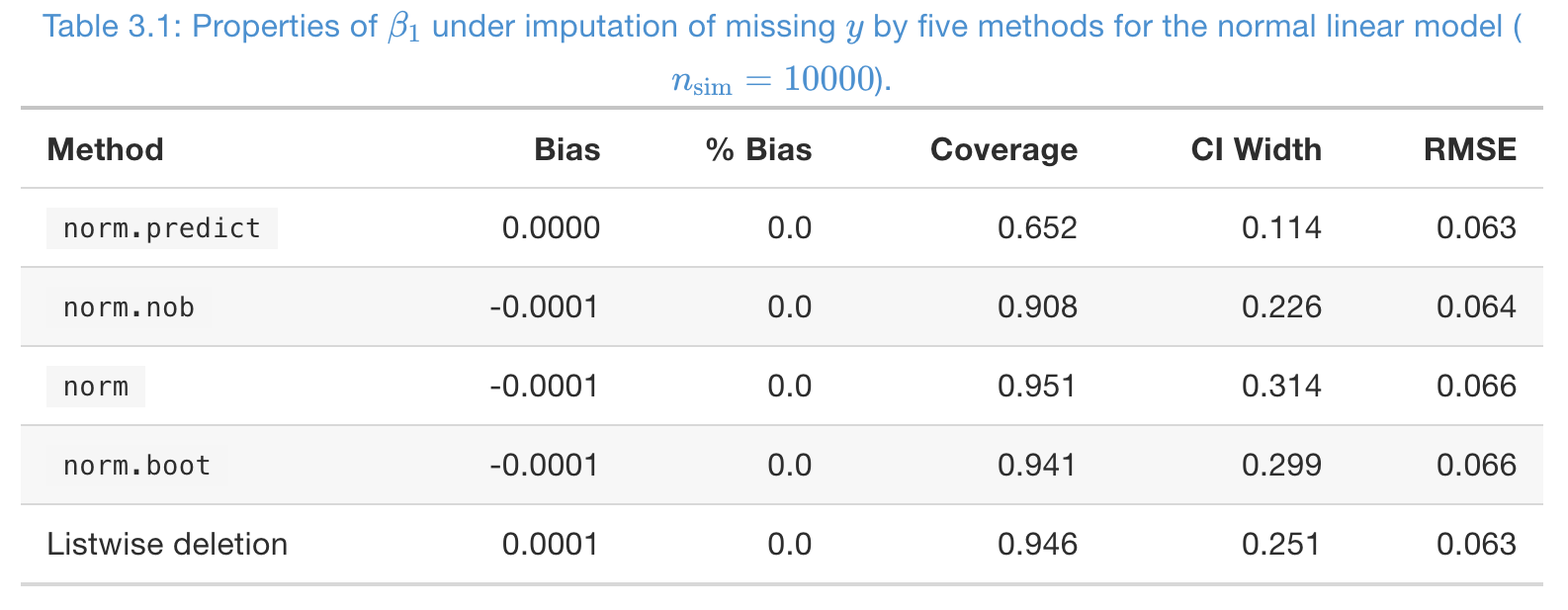
A simulation study, to impute MCAR missing in
- Missing rate in , and number of imputations .
- From coverage,
norm,norm.boot, and listwise deletion are good - From CI width, listwise deletion is better than multiple imputation here, but it’s not always this case, especially when the number of covariates is large.
- RMSE is not imformative at all!
- From coverage,
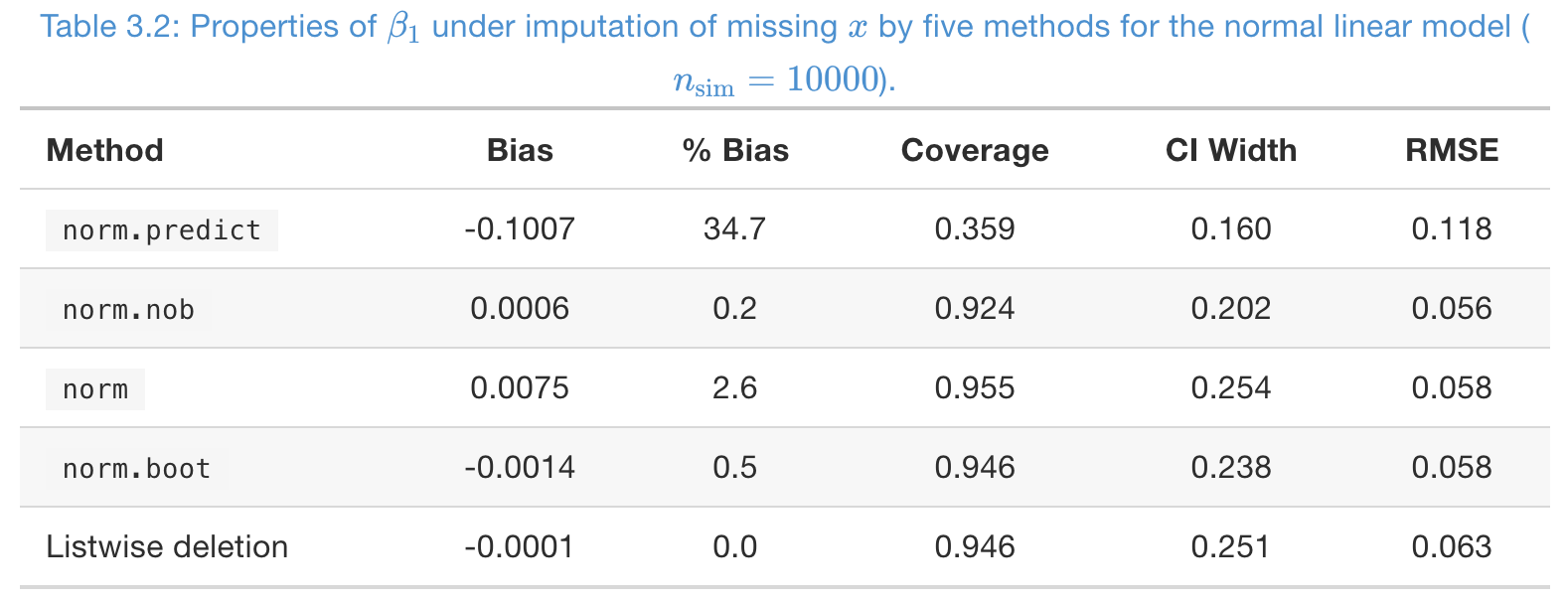
 ### A simulation study, to impute MCAR missing in
### A simulation study, to impute MCAR missing in
- Missing rate in , and number of imputations .
norm.predictis severely biased;normis slightly biased- From coverage,
norm,norm.boot, and listwise deletion are good - Again, RMSE is not imformative at all!
Impute from a (continuous) non-normal distributions
Optional 1: mean predictive matching
- Optional 2: model the non-normal data directly
- E.g., impute from a t-distribution
- The GAMLSS package: extends GLM and GAM
Predictive Mean Matching
Predictive mean matching (PMM), general principle
For each missing entry, the method forms a small set of candidate donors (3, 5, or 10) from completed cases whose predicted values closest to the predicted value for the missing entry
One donor is randomly drawn from the candidates, and the observed value of the donor is taken to replace the missing value
Advantages of predictive mean matching (PMM)
PMM is fairly robust to transformations of the target variable
PMM can also be used for discrete target variables
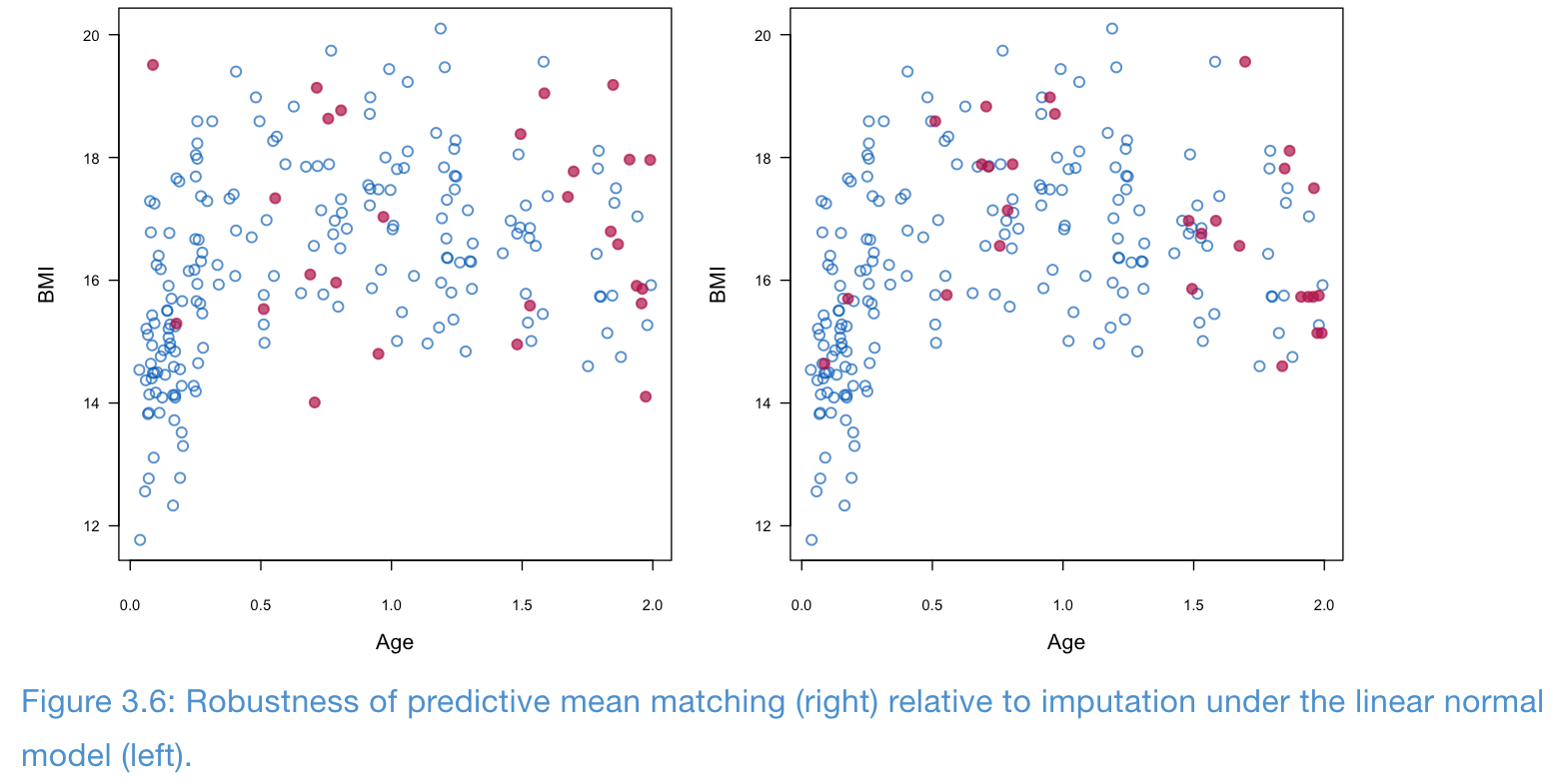
- PMM is fairly robust to model misspecification
- In the following example, the relationship between age and BMI is not linear, but PMM seems to preserve this relationship better than linear normal model
How to select the donors
- Once the metric has been defined, there are four ways to select the donors.
- Let denote the predicted values of rows with observed
- Let denote the predicted values of rows with missing
- Pre-specify a threshold , take all such that as donors, and randomly sample one donor to impute
- Choose the closest candidate as the donor (only 1 donor), also called (nearest neighbor hot deck)
- Pre-specify a number , take the closest candidate as donors, and randomly sample one donor to impute. Usually,
- Sample one donor with a probability that depends on the distance
- Implemented by the
midastouchmethod inmice, and also themidastouchpackage
- Implemented by the
Types of matching
- Type 0: is matched to
- Bad: it ignores the sampling variability in
- Type 1: is matched to
- Here, is a random draw from the posterior distribution
- Good. The default in
mice
- Type 2: is matched to
- Not very ideal, when model is small, the same donors get selected too often
- Type 3: is matched to
- Here, and are two different random draws from the posterior distribution
- Good
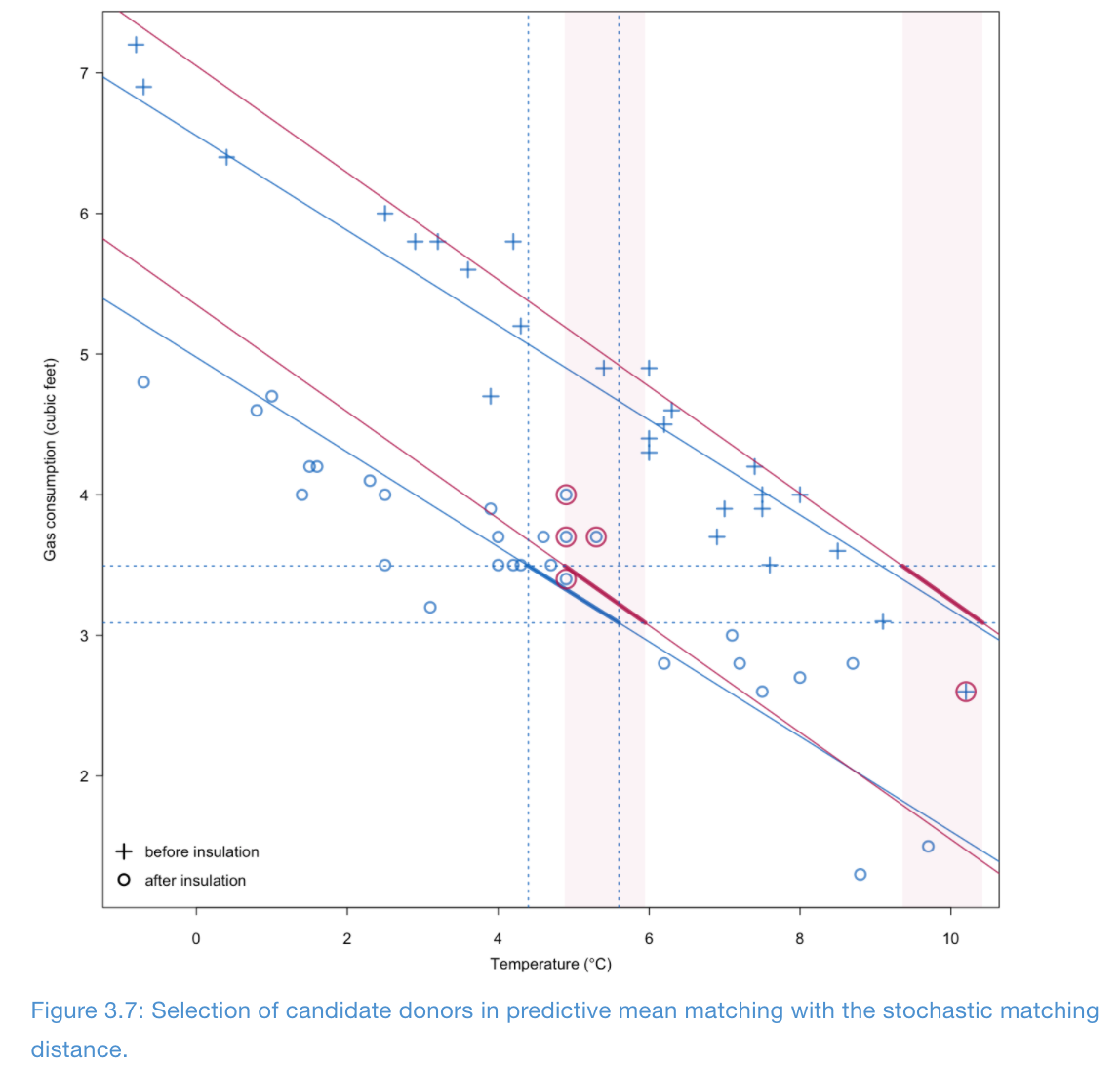
Illustration of Type 1 matching
Number of donors
is too low (bad!). It may select the same donor over and over again
The default in
miceis . Also, are also feasible
Pitfalls of PMM
If the data is small, or if there is a region where the missing rate is high, then the same donors may be used for too many times.
Mis-specification of the impute model
PMM cannot be used to extrapolate beyond the range of the data, or to interpolate within the region where data is sparse
PMM may not perform well with small datasets
Imputation under CART
Multiple imputation under a tree model
missForest: single imputation with CART is bad- Multiple imputation under a tree model using the bootstrap:
- Draw a bootstrap sample among the observed data, and fit a CART model
- For each missing value , find it’s terminal node . All the cases in this node are the donors
Randomly select one donor to impute
- When fitting the tree, it may be useful to pre-set the size of nodes to be 5 or 10
- We can also use random forest instead of CART
Imputing Categorical and Other Types of Data
Imputation under Bayesian GLMs
- Binary data: logistic regression (
logregmethod inmice)- In case of data separation, use a more informative Bayesian prior
Categorical variable with unordered categories: multinomial logit model (
polyregmethod inmicepackage)- Categorical variable with ordered categories: ordered logit model
(
polrmethod inmicepackage)- For identifiability, set
When impute from these GLM models, make sure to not use the MLE of parameters, but either a draw from posterior, or a bootstraped estimate.
Categorical variables are harder to impute than continuous ones
- Empirically, the GLM imputations do not perform well
- If missing rate exceeds 0.4
- If the data is imbalanced
- If there are many categories
- GLM imputation is found inferior than CART or latent class models
Imputation of count data
- Option 1: predictive mean matching
- Option 2: ordered categorical imputation
- Option 3: (zero-inflated) Poisson regression
- Option 4: (zero-inflated) negative binomial regression
Imputation of semi-continuous data
Semi-continuous data: has a high mass at one point (often zero) and a continuous distribution over the remaining values
- Option 1: model the data in two parts: logistic regression + regression
Option 2: predictive mean matching
References
Van Buuren, S. (2018). Flexible Imputation of Missing Data, 2nd Edition. CRC press.