Week 3. Search
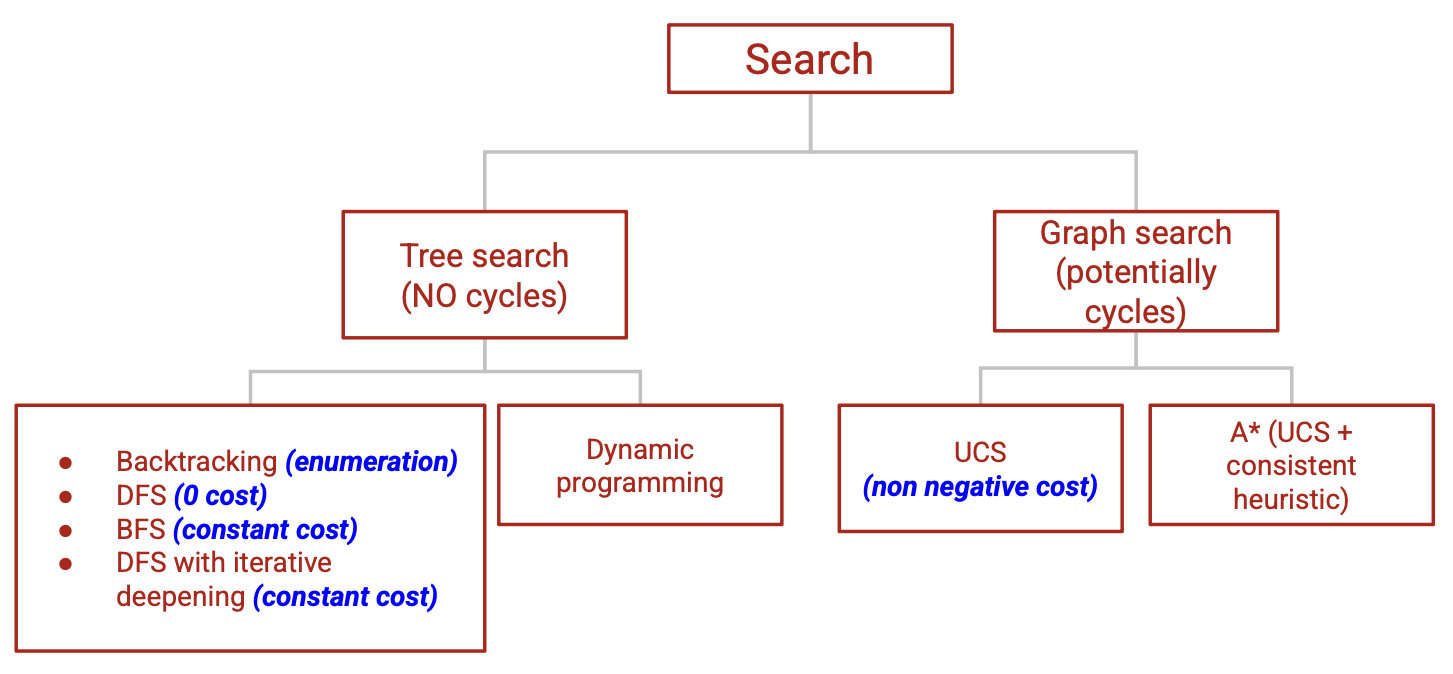
Figure source: Stanford CS221 spring 2025, Problem Workout 3 Slides
Note: DP is not necessarily a tree search algorithm. It’s a technique used to solve problems efficiently by breaking them down into smaller sub-problems. It can be applied to both tree search and graph search.
A good reference: state-based models cheetsheet
Tree Search
Model a search problem
Defining a search problem
- : stating state.
- Actions: possible actions
- Cost: action cost
- Succ: the successor state
- IsEnd: reached end state?
A search tree
- Node: a state
- Edge: an (action, cost) pair
- Root: starting state
- Leaf nodes: end states
Each root-to-leaf path represents a possible action sequence, and the sum of the costs of the edges is the cost of that path
Objective: find a minimal cost path to the end state
Coding a search problem: a class with the following methods:
stateState() -> StateisEnd(State) -> boolsuccAndCost(State) -> List[Tuple[str, State, float]]returns a list of(action, state, cost)tuples.
Tree search algorithms
- : actions per state, maximum depth, depth of the solution path
| Algorithm | Idea | Action costs | Space | Time |
|---|---|---|---|---|
| Backtracking search | Any cost | |||
| Depth-first search | Backtracking + stop when find the first end state | All costs = 0 | ||
| Breadth-first search | Explore in order of increasing depth | Constant cost | ||
| DFS with iterative deepening | Call DFS for maximum depths 1, 2, | Constant cost |
- Always exponential time
- Avoid exponential spaces with DFS-ID
Dynamic Programming
Dynamic programming (DP)
- A backtracking search algorithm with memorization (i.e. partial results are saved)
- May avoid the exponential running time of tree search
- Assumption: acyclic graph, so there is always a clear order in which to compute all the future (or past) costs.
For any given state , the DP future cost is
Note that for DP, we can analogously define .
A state is a summary of all the past actions sufficient to choose future actions optimally.
Graph Search
- total states, of which are closer than end state
| Algorithm | Cycles? | Idea | Action costs | Time/space |
|---|---|---|---|---|
| Dynamic programming | No | Save partial results | Any | |
| Uniform cost search | Yes | Enumerates states in order of increasing past cost |
- Exponential savings compared with tree search!
- Graph search: can have cycles
Uniform cost search (UCS)
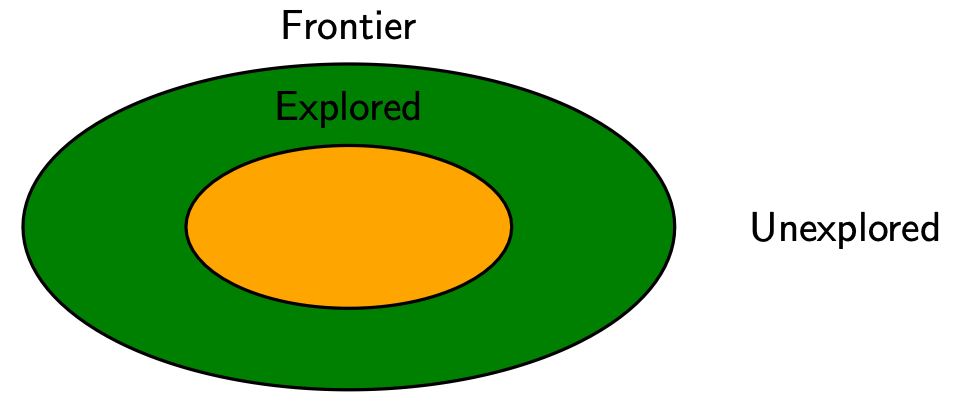
Figure source: Stanford CS221 spring 2025, lecture slides week 3
Types of states
- Explored: optimal path found; will not update cost to these states in the future
- Frontier: states we’ve seen, but still can update the cost of how to get there cheaper (i.e., priority queue)
- Unexplored: states we haven’t seen
Uniform cost search (UCS) algorithm
- Add to frontier
- Repeat until fronteir is empty:
- Remove with smallest priority (minimum cost to among visited paths) from frontier
- If : return solution
- Add to explored
- For each action :
- Get successor
- If is already in explored: continue
- Update frontier with and priority with (if it’s cheaper)
Properties of UCS
Correctness: When a state is popped from the frontier and moved to explored, its priority is PastCost, the minimum cost to .
USC potentially explores fewer states, but requires move overhead to maintain the priority queue
A*
A* algorithm: Run UCS with modified edge costs
- USC: explore states in order of PastCost
- A*: explore states in order of PastCost
- is a heuristic that estimates FutureCost
Heuristic
Consistency:
- Triangle inequality: , and

Figure source: Stanford CS221 spring 2025, lecture slides week 3
Admissibility:
If is consistent, then it is admissible.
A* properties
- Correctness: if is consistent, then A* returns the minimum cost path
- Efficiency: A* explores all states satisfying
- If , then A* is the same as UCS
- If , then A* only explores nodes on a minimum cost path
- Usually somewhere in between
Create via relaxation
- Remove constraints
- Reduce edge costs (from to some finite cost)
Week 4. Markov Decision Processes
- Uncertainty in the search process
- Performing action from a state can lead to several states in a probabilistic manner.
- The probability and reward of each pair may be known or unknown.
- If known: policy evaluation, value iteration
- If unknown: reinforcement learning
Markov Decision Processes (offline)
Model an MDP
- Markove decision process definition:
- States: the set of states
- : stating state.
- Actions: possible actions
- : transition probability of if take action in state
- Reward: reward for the transition
- IsEnd: reached end state?
- : discount factor
- A policy : a mapping from each state to an action
Policy Evaluation (on-policy)
Utility of a policy is the discounted sum of the rewards on the path
- Since the policy yields a random path, its utility is a random variable
For a policy, its path is (action, reward, new state) tuple, then the utility with discount is
: the expected utility (called value) of a policy from state
: Q-value, the expected utility of taking action from state , and then following policy
Connections between and :
Iterative algorithm for policy evaluation
- Initialize for all
- For iteration :
- For each state ,
Choice of : stop when values don’t change much
MDP time complexity is , where is the number of states and is the number of with
Value Iteration (off-policy)
Optimal value : maximum value attained by any policy
Optimal Q-value
- Value iteration algorithm:
- Initialize for all
- For iteration :
- For each state ,
- VI time complexity is , where is the number of states, is the number of actions, and is the number of with
Reinforcement Learning (online)
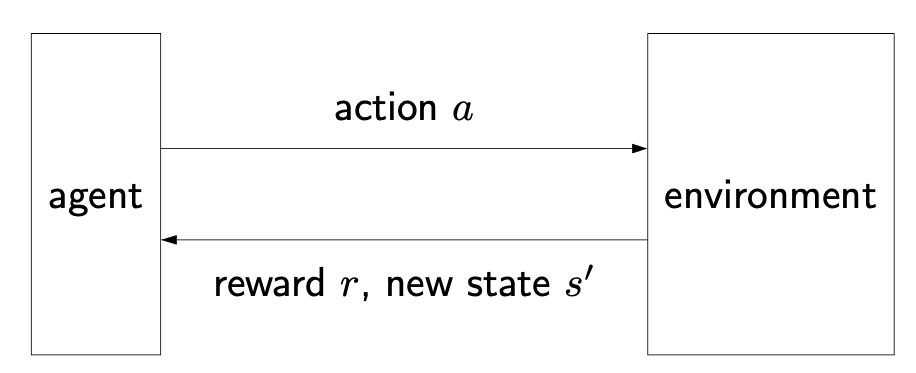
Figure source: Stanford CS221 spring 2025, lecture slides week 4
- Summary of reinforcement learning algorithms
| Algorithm | Estimating | Based on |
|---|---|---|
| Model-based Monte Carlo | ||
| Model-free Monte Carlo | ||
| SARSA | ||
| Q-learning |
Model-based methods (off-policy)
- Based on data , estimate the transition probabilities and rewards of the MDP
- If is a non-deterministic policy which allows us to explore each (state, action) pair infinitely often, then the estimates of the transitions and rewards will converge.
- Thus, the estimates and are not necessarily policy dependent. So model-based methods are off-policy estimations.
Model-free Monte Carlo (on-policy)
The main idea is to estimate the Q-values directly
Original formula
Equivalent formulation: for each , let
- Implied objective: least squares
SARSA (on-policy)
- SARSA algorithm
On each :
- SARSA uses estimates instead of just raw data
| Model-free Monte Carlo | SARSA |
|---|---|
| based on one path | based on estimate |
| unbiased | biased |
| large variance | small variance |
| wait until end of update | can update immediately |
Q-learning (off-policy)
On each :
Epsilon-greedy
Reinforcement learning algorithm template
- For
- Choose action
- Receive reward and observe new state
- Update parameters
- For
What exploration policy to use? Need to balance exploration and exploitation.
Epsilon-greedy policy
Function appxomation
- Large state spaces is hard to explore.For better generalization to handle unseen states/actions, we can use function approximation, to define
- features , and
- weights , such that
- Q-learning with function approximation: on each ,
Week 5. Games
Modeling Games
- A simple example game

Figure source: Stanford CS221 spring 2025, lecture slides week 5
- Game tree
- Each node is a decision point for a player
- Each root-to-leaf path is a possible outcome of the game
- Nodes to indicate certain policy: use for maximum node (agent maximize his utility) and for minimum node (opponent minimizes agent’s utility)
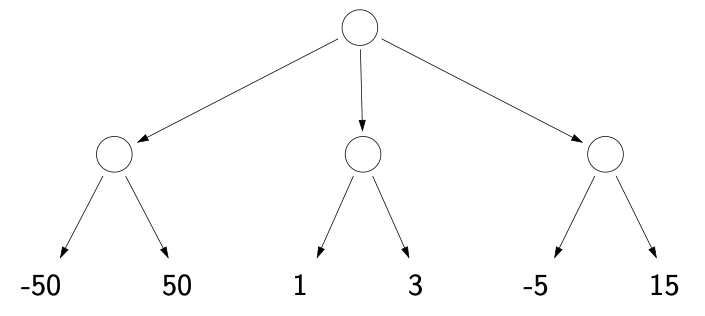
Figure source: Stanford CS221 spring 2025, lecture slides week 5
Two-player zero-sum game:
- Actions
- Succ
- IsEnd
- Utility: agent’s utility for end state
- Player: player who controls state s
- Players
- Zero-sum: utility of the agent is negative the utility of the opponent
Property of games
- All the utility is at the end state
- For a game about win/lose at the end (e.g., chess), Utility is (if agent wins), (if opponent wins), or (if draw).
- Different players in control at different state
- All the utility is at the end state
Policies (for player in state )
- Deterministic policy:
- Stochastic policy: , a probability
Game Algorithms
Game evaluation
- Use recurrence for policy evaluation to estimate value of the game (expected utility):
Expectimax
- Expectimax: given opponent’s policy, find the best policy for the agent
Minimax
- Minimax assumes the worst case for the opponent’s policy
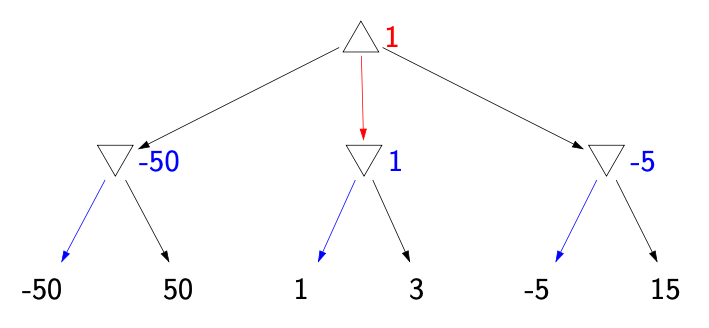
Figure source: Stanford CS221 spring 2025, lecture slides week 5
Minimax properties
- Best against minimax opponent
- Lower bound against any opponent
- Not optimal if opponent is known! Here, stands for an arbitrary known policy, for example, random choice with equal probabilities.
Relationship between game values

Figure source: Stanford CS221 spring 2025, lecture slides week 5
Expectiminimax
- Modify the game to introduce randomness

Figure source: Stanford CS221 spring 2025, lecture slides week 5
- This is equivalent to having a third player, the coin
Evaluation functions
Computation complexity: with branching factor and depth (number of turns because of two players), since this is a tree search, we have
- space
- time
Limited depth tree search: stop at maximum depth
- Use: at state , call
An evaluation function Eval is a possibly very weak estimate of the value , using domain knowledge
- This is similar to FutureCost in the A* search problems. But unlike A*, there are no guarantees on the error for approximation.
Alpha-Beta pruning
Branch and bound
- Maintain lower and upper bounds on values.
- If intervals don’t overlap, then we can choose optimally without future work
Alpha-beta prining for minimax:
- : lower bound on value of max node
- : upper bound on value of min node
- Store and
- Prune a node if its interval doesn’t have non-trivial overlap with every ancestor
Pruning depends on the order
- Worse ordering: time
- Best ordering: time
- Random ordering: time, when
- In practice, we can order based on the evaluation function Eval:
- Max nodes: order successors by decreasing Eval
- Min nodes: order successors by increasing Eval
More Topics
TD learning (on-policy)
General learning framework
- Objective function
- Update
Temporal difference (TD) learning: on each ,
- For linear function
Simultaneous games
Payoff matrix: for two players, is A’s utility if A chooses action and B chooses action
Strategies (policies)
- Pure strategy: a single action
- Mixed strategy: a probability distribution of actions
Game evaluation: the value of the game if player A follows and player B follows is
For pure strategies, going second is no worse
Mixed strategy: second play can play pure strategy: for any fixed mixed strategy , can be obtained by a pure strategy
Minimax theorem: for every simultaneous two-player zero-sum game with a finite number of actions
- Revealing your optimal mixed strategy doesn’t hurt you.