High level summaries
- State-based models: search problems, MDPs, games
- Applications: route finding, game playing, etc
- Terms: states, actions, costs
- Variable-based models: CSPs, Bayesian networks
- Applications: scheduling, tracking, medical diagnosis, etc
- Terms: variables, factors
- Logic-based models: propositional logic, first-order logic
- Applications: theorem proving, verification, etc
- Terms: logical formulas, inference rules
- Problems with logic:
- Deterministic, cannot handle uncertainty
- Rule-based, does not allow to learn from data
- State-based models: search problems, MDPs, games
Propositional Logic
Propositional symbols (atomic formulas):
Use Logical connectives to build up formulas recursively: if and are formulas, so are the following
- Negation:
- Conjunction:
- Disjunction:
- Implication:
- Bicodintional:
Models
Model : an assignment of values to propositional symbols
Interpretation function: for a formula and a model ,
- Define
Knowledge base
Knowledge base KB:
Add a formula to the knowledge base:
- From KB to KB
- Shrinks the set of models: from to
Relationships between a KB and a formula
| Relationship | Notation | Definition | Meaning |
|---|---|---|---|
| Entailment | KB | Already knew that. | |
| Contradiction | Don’t believe that. | ||
| Contingency | Learned something new. | ||
| Inference |
KB contradicts with KB entails
Probabilistic interpretation
A KB is satisfiable if
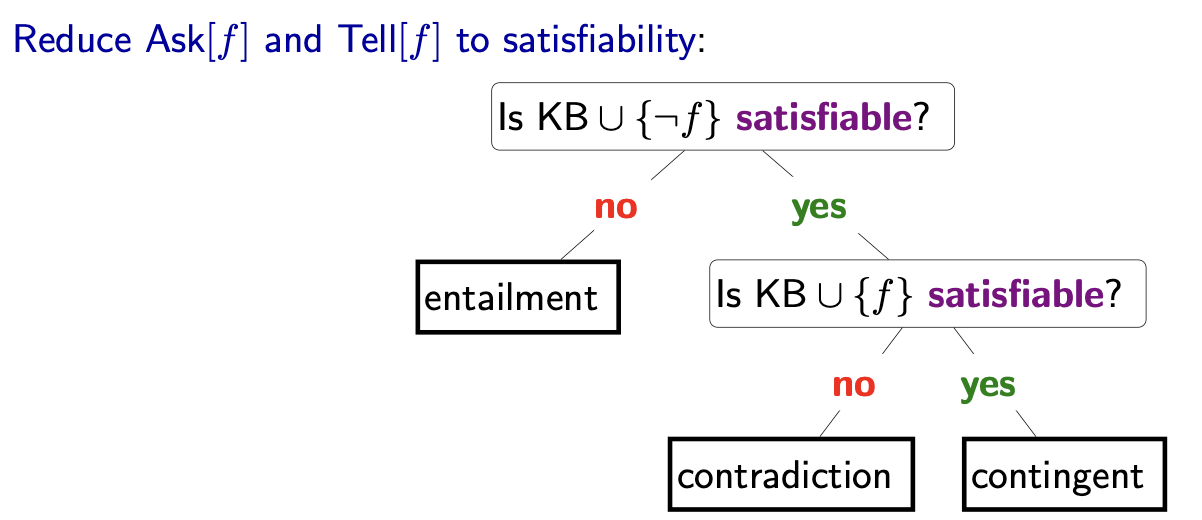
Figure source: Stanford CS221 spring 2025, lecture slides week 9
Checking satisfiability (SAT) in propositional logic is a special case of CSPs
Logic term Counterpart CSP term propositional symbol variable formula constraint model assignment
Inference Rules
Inference rule: if the premises are in the KB, then your can add the conclusion to the KB. Formula:
Modus ponens inference rule: captures the if-then reasoning pattern. For any propositional symbols and , we have
Derivation: KB derives , written as , iff eventually gets added to KB.
- Inference rules operate directly on syntax, not on semantics.
Soundness and completeness
- A set of inference rules is sound if
- Nothing but the truth
- Showing soundness is easy
- A set of inference rules is complete if
- Whole truth
- Showing completeness if hard
- Fixing completeness
- Option 1: restrict the allowed set of formulas, to propositional logic with only Horn clauses
- Option 2: use more powerful inference rules, change from Modus ponens to resolution
| Formulas allowed | Inference rules | Complete? |
|---|---|---|
| Propositional logic | modus ponens | No |
| Propositional logic (only Horn clauses) | modus ponens | Yes |
| Propositional logic | resolution | Yes |
Propositional Modus Ponens
Horn clauses: is either a definite clause, or a goal clause
A more generic version of the modus ponens inference rule
Theory: Modus ponens is complete with respect to Horn clauses. This is, if KB contains only Horn clauses, then
Propositional Resolution
- Rewrite implication to disjunction
- In this way, we can rewrite modus ponens as Note that and are cancelled out.
- Resolution inference rule: cancel out and in the middle
Conjunctive normal form (CNF)
CNF is a conjunction () of clauses ()
Every formula in propositional logic can be converted into an equivalent CNF formula
Conversion rules
Propositional logic CNF
Proof by Resolution
- Add into KB
- Convert all formulas into CNF
- Repeatedly apply resolution rule
- Return entailment iff derive false
First-order Logic
- Syntax of first-order logic
- Terms (object)
- constant symbol (e.g., arithmetic)
- variable (e.g., )
- function of terms (e.g., Sum(3, ))
- Formulas (truth values)
- Atomic formulas (atoms): predicate applied to terms, e.g., Knows(, arithmetic)
- Connectives applied to formulas: e.g., Student() Knows(, arithmetic)
- Quantifiers applied to formulas: e.g., Student() Knows(, arithmetic)
- Terms (object)
- Quantifiers: for all () and exists ()
- Note the different connectives:
- Student Knows(, arithmetic)
- Student Knows(, arithmetic)
- Note the different connectives:
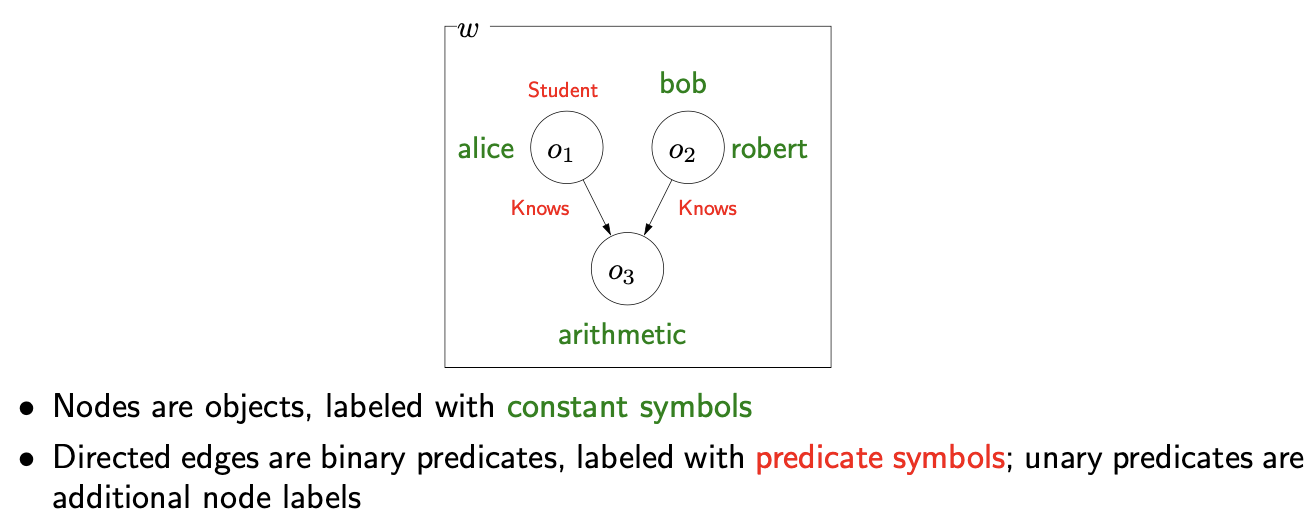
Figure source: Stanford CS221 spring 2025, lecture slides week 9
First-order Modus Ponens
Definite clause in first-order logic for variables and atomic formuas which contain those variables, has the following form
Substitution is a mapping from variables to terms Subst returns the result of performing substitution on .
- E.g., Subst
Unification: takes two formulas and and returns a substitution which is the most general unifier:
First-order modus ponens with substitution: Let and , then