For the pdf slides, click here
Variational Inference
Introduction of the variational inference method
Definitions
- Variational inference is also called variational Bayes,
thus
- all parameters are viewed as random variables, and
- they will have prior distributions.
- We denote the set of all latent variables and parameters by Z
- Note: the parameter vector θ no long appears, because it’s now a part of Z
- Goal: find approximation for
- posterior distribution p(Z∣X), and
- marginal likelihood p(X), also called the model evidence
Model evidence equals lower bound plus KL divergence
Goal: We want to find a distribution q(Z) that approximates the posterior distribution p(Z∣X). In other word, we want to minimize the KL divergence KL(q‖p).
Note the decomposition of the marginal likelihood logp(X)=L(q)+KL(q‖p),
Thus, maximizing the lower bound (also called ELBO) L(q) is equivalent to minimizing the KL divergence KL(q‖p). L(q)=∫q(Z)log{p(X,Z)q(Z)}dZKL(q‖p)=−∫q(Z)log{p(Z∣X)q(Z)}dZ
Mean field family
Goal: restrict the family of distribution q(Z) so that they comprise only tractable distributions, while allow the family to be sufficiently flexible so that it can approximate the posterior distribution well
- Mean field family : partition the elements of Z into disjoint groups
denoted by Zj, for j=1,…,M, and assume q factorizes wrt these groups:
q(Z)=M∏j=1qj(Zj)
- Note: we place no resitriction on the functional forms of the individual factors qj(Zj)
Solution for mean field families: derivation
We will optimize wrt each qj(Zj) in turn.
For qj, the lower bound (to be maximized) can be decomposed as L(q)=∫∏kqk{logp(X,Z)−∑klogqk}dZ=∫qj{∫logp(X,Z)∏k≠jqkdZk}⏟Ek≠j[logp(X,Z)]dZj−∫qjlogqjdZj+const=−KL(qj‖˜p(X,Zj))+const
- Here the new distribution ˜p(X,Zj) is defined as log˜p(X,Zj)=Ek≠j[logp(X,Z)]+const
Solution for mean field families
A general expression for the optimal solution q∗j(Zj) is logq∗j(Zj)=Ek≠j[logp(X,Z)]+const
- We can only use this solution in an iterative manner, because the expectations should be computed wrt other factors qk(Zk) for k≠j.
- Convergence is guaranteed because bound is convex wrt each factor qj
- On the right hand side we only need to retain those terms that have some functional dependence on Zj
Example: approximate a bivariate Gaussian using two independent distributions
Target distribution: a bivariate Gaussian p(z)=N(z∣μ,Λ−1),μ=(μ1μ2),Λ=(λ11λ12λ12λ22)
We use a factorized form to approximate p(z): q(z)=q1(z1)q2(z2)
Note: we do not assume any functional forms for q1 and q2
VI solution to the bivariate Gaussian problem
logq∗1(z1)=Ez2[logp(z)]+const=Ez2[−12(z1−μ1)2Λ11−(z1−μ1)Λ12(z2−μ2)]+const=−12z21Λ11+z1μ1Λ11−(z1−μ1)Λ12(E[z2]−μ2)+const
Thus we identify a normal, with mean depending on E[z2]: q∗(z1)=N(z1∣m1,Λ−111),m1=μ1−Λ−111Λ12(E[z2]−μ2)
By symmetry, q∗(z2) is also normal; its mean depends on E[z1] q∗(z2)=N(z2∣m2,Λ−122),m2=μ2−Λ−122Λ12(E[z1]−μ1)
We treat the above variational solutions as re-estimation equations, and cycle through the variables in turn updating them until some convergence criterion is satisfied
Visualize VI solution to bivariate Gaussian
Variational inference minimizes KL(q‖p): mean of the approximation is correct, but variance (along the orthogonal direction) is significantly under-estimated
Expectation propagation minimizes KL(p‖q): solution equals marginal distributions
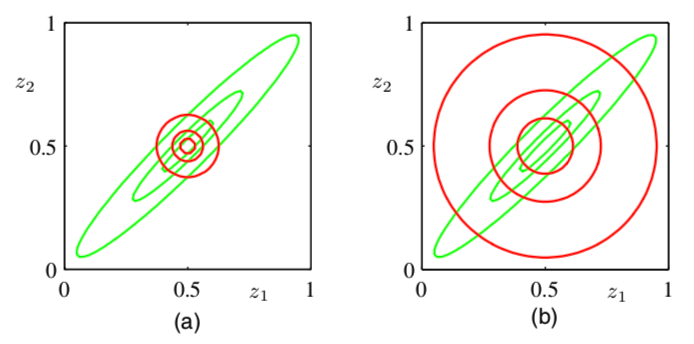
Figure 1: Left: variational inference. Right: expectation propagation
Another example to compare KL(q‖p) and KL(p‖q)
- To approximate a mixture of two Gaussians p (blue contour)
- Use a single Gaussian q (red contour) to approximate p
- By minimizing KL(p‖q): figure (a)
- By minimizing KL(q‖p): figure (b) and (c) show two local minimum
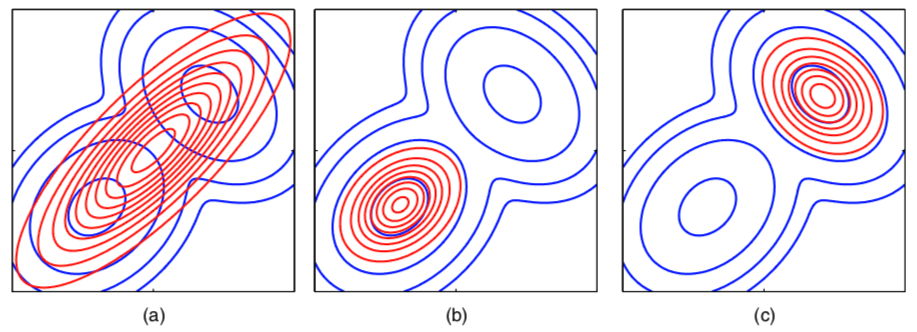
- For multimodal distribution
- a variational solution will tend to find one of the modes,
- but an expectation propagation solution would lead to poor predictive distribution (because the average of the two good parameter values is typically itself not a good parameter value)
Example: univariate Gaussian
Example: univariate Gaussian
Suppose the data D={x1,…,xN} follows iid normal distribution xi∼N(μ,τ−1)
The prior distributions are μ∣τ∼N(μ0,(λ0τ)−1)τ∼Gam(a0,b0)
Factorized variational approximation q(μ,τ)=q(μ)q(τ)
Variational solution for μ
logq∗(μ)=Eτ[logp(D∣μ,τ)+logp(μ∣τ)]+const=−E[τ]2{λ0(μ−μ0)2+N∑i=1(xi−μ)2}+const
Thus, the variational solution for μ is q(μ)=N(μ∣μN,λ−1N)μN=λ0μ0+Nˉxλ0+NλN=(λ0+N)E[τ]
Variational solution for τ
logq∗(τ)=Eμ[logp(D∣μ,τ)+logp(μ∣τ)+logp(τ)]+const=(a0−1)logτ−b0τ+N2logτ −τ2Eμ[λ0(μ−μ0)2+N∑i=1(xi−μ)2]+const
Thus, the variational solution for τ is q(τ)=Gam(τ∣aN,bN)aN=a0++N2bN=b0+12Eμ[λ0(μ−μ0)2+N∑i=1(xi−μ)2]
Visualization of VI solution to univariate normal
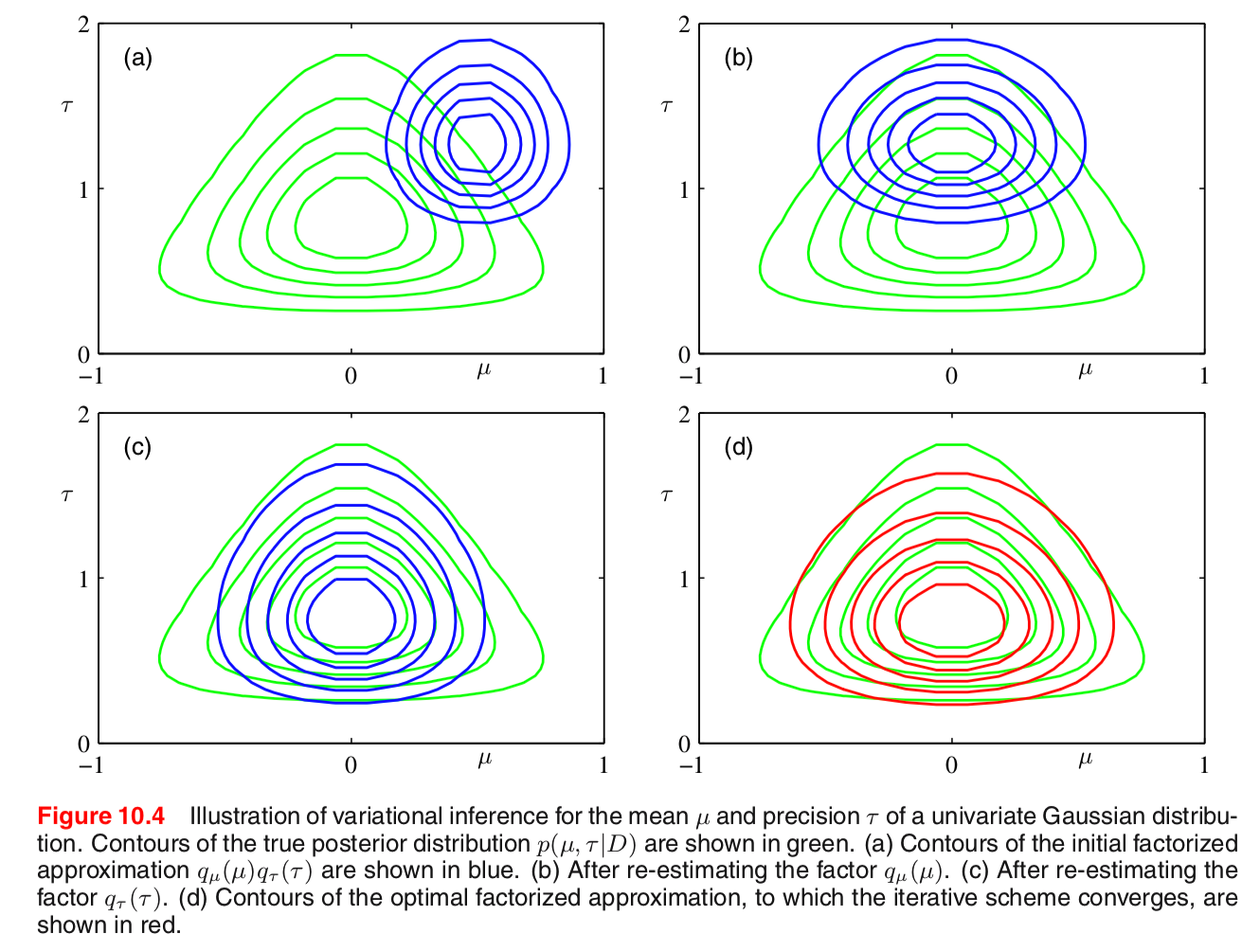
Model selection
Model selection (comparison) under variational inference
In addition to making inference on the parameter Z, we may also want to compare a set of candidate models, denoted by index m
We should consider the factorization q(Z,m)=q(Z∣m)q(m) to approximate the posterior p(Z,m∣X)
We can maximize the information lower bound Lm=∑m∑Zq(Z∣m)q(m)log{p(Z,X,m)q(Z∣m)q(m)} which is a lower bound of logp(X)
The maximized q(m) can be used for model selection
Variational Mixture of Gaussians
Mixture of Gaussians
For each observation xn∈RD, we have a corresponding latent variable zn, a 1-of-K binary group indicator vector
Mixture of Gasussians joint likelihood, based on N observations p(Z∣π)=N∏n=1K∏k=1πznkkp(X∣Z,μ,Λ)=N∏n=1K∏k=1N(xn∣μk,Λ−1k)znk
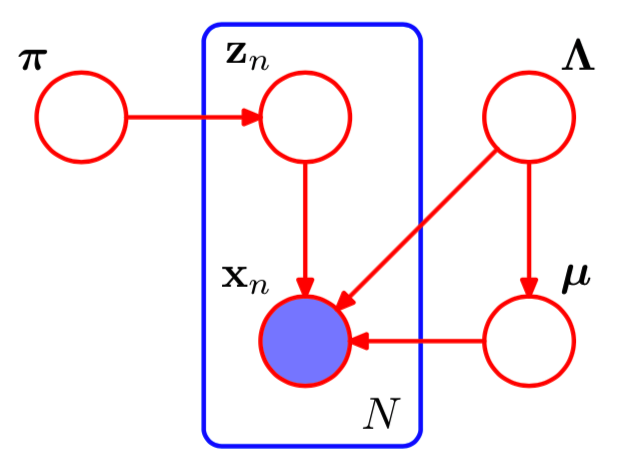
Figure 2: Graph representation of mixture of Gaussians
Conjugate priors
Dirichlet for π p(π)=Dir(π∣α0)∝K∏k=1πα0k−1k
Independent Gaussian-Wishart for μ,Λ p(μ,Λ)=K∏k=1p(μk∣Λk)p(Λk)=K∏k=1N(μk∣m0,(β0Λk)−1)W(Λk∣W0,ν0)
- Usually, the prior mean m0=0
Variational distribution
Joint posterior p(X,Z,π,μ,Λ)=p(X∣Z,μ,Λ)p(Z∣π)p(π)p(μ∣Λ)p(Λ)
Variational distribution factorizes between the latent variables and the parameters q(Z,π,μ,Λ)=q(Z)q(π,μ,Λ)=q(Z)q(π)K∏k=1q(μk,Λk)
Variational solution for Z
Optimized factor logq∗(Z)=Eπ,μ,Λ[logp(X,Z,π,μ,Λ)]=Eπ[logp(Z∣π)]+Eμ,Λ[logp(X∣Z,μ,Λ)]=N∑n=1K∑k=1znklogρnk+constlogρnk= E[logπk]+12E[log|Λk|]−D2log(2π)−12Eμ,Λ[(xn−μk)′Λk(xn−μk)]
Thus, the factor q∗(Z) takes the same functional form as the prior p(Z∣π) q∗(Z)=N∏n=1K∏k=1rznknk,rnk=ρnk∑Kj=1ρnj
- By q∗(Z), the posterior mean (i.e., responsibility) E[znk]=rnk
Define three statistics wrt the responsibilities
- For each of group k=1,…,K, denote Nk=N∑n=1rnkˉxk=1NkN∑n=1rnkxnSk=1NkN∑n=1rnk(xn−ˉxk)(xn−ˉxk)′
Variational solution for π
Optimized factor logq∗(π)=logp(π)+EZ[p(Z∣π)]=(α0−1)K∑k=1logπk+K∑k=1N∑n=1rnklogπnk+const
Thus, q∗(π) is a Dirichlet distribution q∗(π)=Dir(α),αk=α0+Nk
Variational solution for μk,Λk
Optimized factor for (μk,Λk) logq∗(μk,Λk)= EZ[N∑n=1znklogN(xn∣μk,Λ−1k)]+logp(μk∣Λk)+logp(Λk)
Thus, q∗(μk,Λk) is Gaussian-Wishart q∗(μk∣Λk)=N(mk,(βkΛk)−1)q∗(Λk)=W(Λk∣Wk,νk)
Parameters are updated by the data βk=β0+Nk,mk=1βk(β0m0+Nkˉxk),νk=ν0+NkW−1k=W−10+NkSk+β0Nkβ0+Nk(ˉxk−m0)(ˉxk−m0)′
Similarity between VI and EM solutions
Optimization of the variational posterior distribution involves cycling between two stages analogous to the E and M steps of the maximum likelihood EM algorithm
- Finding q∗(Z): analogous to the E step, both need to compute the responsibilities
- Finding q∗(π,μ,Λ): analogous to the M step
The VI solution (Bayesian approach) has little computational overhead, comparing with the EM solution (maximum likelihood approach). The dominant computational cost for VI are
- Evaluation of the responsibilities
- Evaluation and inversion of the weighted data covariance matrices
Advantage of the VI solution over the EM solution:
- Since our priors are conjugate, the variational posterior distributions have the same functional form as the priors
No singularity arises in maximum likelihood when a Gassuain component “collapses” onto a specific data point
- This is actually the advantage of Bayesian solutions (with priors) over frequentist ones
No overfitting if we choose a large number K. This is helpful in determining the optimal number of components without performing cross validation
- For α0<1, the prior favors soutions where some of the mixing coefficients π are zero, thus can result in some less than K number components having nonzero mixing coefficients
Computing variational lower bound
- To test for convergence, it is useful to monitor the bound during the re-estimation.
- At each step of the iterative re-estimation, the value of the lower bound should not decrease L= ∑Z∭
Label switching problem
EM solution of maximum likelihood does not have label switching problem, because the initialization will lead to just one of the solutions
In a Bayesian setting, label switching problem can be an issue, because the marginal posterior is multi-modal.
Recall that for multi-modal posteriors, variational inference usually approximate the distribution in the neighborhood of one of the modes and ignore the others
Induced factorizations
Induced factorizations: the additional factorizations that are a consequence of the interaction between
- the assumed factorization, and
- the conditional independence properties of the true distribution
For example, suppose we have three variation groups \mathbf{A}, \mathbf{B}, \mathbf{C}
- We assume the following factorization q(\mathbf{A}, \mathbf{B}, \mathbf{C}) = q(\mathbf{A}, \mathbf{B})q(\mathbf{C})
- If \mathbf{A} and \mathbf{B} are conditional independent \mathbf{A} \perp \mathbf{B} \mid \mathbf{X}, \mathbf{C} \Longleftrightarrow p(\mathbf{A}, \mathbf{B} \mid \mathbf{X}, \mathbf{C}) = p(\mathbf{A}\mid \mathbf{X}, \mathbf{C}) p(\mathbf{B} \mid \mathbf{X}, \mathbf{C}) then we have induced factorization q^*(\mathbf{A}, \mathbf{B}) = q^*(\mathbf{A}) q^*(\mathbf{B}) \begin{align*} \log q^*(\mathbf{A}, \mathbf{B}) &= \mathbb{E}_{\mathbf{C}}\left[ \log p(\mathbf{A}, \mathbf{B} \mid \mathbf{X}, \mathbf{C}) \right] + \text{const}\\ &= \mathbb{E}_{\mathbf{C}}\left[ \log p(\mathbf{A} \mid \mathbf{X}, \mathbf{C}) \right] + \mathbb{E}_{\mathbf{C}}\left[ \log p(\mathbf{B} \mid \mathbf{X}, \mathbf{C}) \right] + \text{const}\\ \end{align*}
Variational Linear Regression
Bayesian linear regression
Here, I use a denotion system commonly used in statistics textbooks. So its different from the one used in this book.
Likelihood function p(\mathbf{y} \mid \boldsymbol\beta) = \prod_{n=1}^N \text{N}\left(y_n \mid \mathbf{x}_n \boldsymbol\beta, \phi^{-1}\right)
- \phi = 1/ \sigma^2 is the precision parameter. We assume that it is known.
- \boldsymbol\beta \in \mathbb{R}^p includes the intercept
Prior distributions: Normal Gamma \begin{align*} p(\boldsymbol\beta \mid \kappa) &= \text{N}\left(\boldsymbol\beta \mid \mathbf{0}, \kappa^{-1} \mathbf{I}\right)\\ p(\kappa) &= \text{Gam}(\kappa \mid a_0, b_0) \end{align*}
Variational solution for \kappa
Variational posterior factorization q(\boldsymbol\beta, \kappa) = q(\boldsymbol\beta) q(\kappa)
Varitional solution for \kappa \begin{align*} \log q^*(\kappa) &= \log p(\kappa) + \mathbb{E}_{\boldsymbol\beta}\left[\log p(\boldsymbol\beta \mid \kappa) \right]\\ &= (a_0 - 1)\log \kappa - b_0 \kappa + \frac{p}{2}\log \kappa - \frac{\kappa}{2}\mathbb{E}\left[\boldsymbol\beta'\boldsymbol\beta\right] \end{align*}
Varitional posterior is a Gamma \begin{align*} \kappa & \sim \text{Gam}\left(a_N, b_N\right)\\ a_N & = a_0 + \frac{p}{2}\\ b_N & = b_0 + \frac{\mathbb{E}\left[\boldsymbol\beta'\boldsymbol\beta\right]}{2} \end{align*}
Variational solution for \boldsymbol\beta
Variational solution for \boldsymbol\beta \begin{align*} \log q^*(\boldsymbol\beta) &= \log p(\mathbf{y} \mid \boldsymbol\beta) + \mathbb{E}_{\kappa}\left[\log p(\boldsymbol\beta \mid \kappa) \right]\\ &= -\frac{\phi}{2}\left(\mathbf{y} - \mathbf{X}\boldsymbol\beta \right)^2 - \frac{\mathbb{E}\left[\kappa\right]}{2}\boldsymbol\beta' \boldsymbol\beta\\ &= -\frac{1}{2}\boldsymbol\beta'\left(\mathbb{E}\left[\kappa\right] \mathbf{I} + \phi\mathbf{X}'\mathbf{X} \right)\boldsymbol\beta + \phi\boldsymbol\beta' \mathbf{X}'\mathbf{y} \end{align*}
Variational posterior is a Normal \begin{align*} \boldsymbol\beta &\sim \text{N}\left(\mathbf{m}_N, \mathbf{S}_N \right)\\ \mathbf{S}_N &= \left(\mathbb{E}\left[\kappa\right] \mathbf{I} + \phi\mathbf{X}'\mathbf{X} \right)^{-1}\\ \mathbf{m}_N &= \phi \mathbf{S}_N \mathbf{X}'\mathbf{y} \end{align*}
Iteratively re-estimate the variational solutions
Means of the variational posteriors \begin{align*} \mathbb{E}[\kappa] & = \frac{a_N}{b_N}\\ \mathbb{E}[\boldsymbol\beta'\boldsymbol\beta] & = \mathbf{m}_N \mathbf{m}_N' + \mathbf{S}_N\\ \end{align*}
Lower bound of \log p(\mathbf{y}) can be used in convergence monitoring, and also model selection \begin{align*} \mathcal{L} =~& \mathbb{E}\left[\log p(\boldsymbol\beta, \kappa, \mathbf{y}) \right] - \mathbb{E}\left[\log q^*(\boldsymbol\beta, \kappa) \right]\\ =~& \mathbb{E}_{\boldsymbol\beta}\left[\log p(\mathbf{y} \mid \boldsymbol\beta) \right] + \mathbb{E}_{\boldsymbol\beta, \kappa}\left[\log p(\boldsymbol\beta \mid \kappa) \right] + \mathbb{E}_{\kappa}\left[\log p(\kappa) \right]\\ & - \mathbb{E}_{\boldsymbol\beta}\left[\log q^*(\boldsymbol\beta) \right] - \mathbb{E}_{\kappa}\left[\log q^*(\kappa) \right]\\ \end{align*}
TO BE CONTINUED
Exponential Family Distributions
Local Variational Methods
Variational Logistic Regression
Expectation Propagation
References
- Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.