Univariate Smoothing
- Piecewise linear basis: tent functions
- Penalty to control wiggliness
Additive Models
Generalized Additive Models
Introducing Package mgcv

For the pdf slides, click here

Introduction of GAM

In general the GAM model has a following structure $g (μ_{i}) = A_{i} θ + f_{1} (x_{1 i}) + f_{2} (x_{2 i}) + f_{3} (x_{3 i}, x_{4 i}) + \dots$
- $Y_{i}$ follows some exponential family distribution: $Y_{i} \sim E F (μ_{i}, ϕ)$
- $μ_{i} = E (Y_{i})$
- $A_{i}$ is a row of the model matrix, and $θ$ is the corresponding parameter vector
- $f_{j}$ are smooth functions of the covariates $x_{k}$
This chapter
- Illustrates GAMs by basis expansions, each with a penalty controlling function smoothness
- Estimates GAMs by penalized regression methods
Takeaway: technically GAMs are simply GLM estimated subject to smoothing penalties

Univariate Smoothing

Piecewise linear basis: tent functions

Representing a function with basis expansions

Let’s consider a model containing one function of one covariate $y_{i} = f (x_{i}) + ϵ_{i}, ϵ_{i} \overset{iid}{\sim} N (0, σ^{2})$
If $b_{j} (x)$ is the $j$ th basis function, then $f$ is assumed to have a representation $f (x) = \sum_{j = 1}^{k} b_{j} (x) β_{j}$ with some unknown parameters $β_{j}$
- This is clearly a linear model

The problem with polynomials

A $k$ th order polynomial is $f (x) = β_{0} + \sum_{j = 1}^{k} β_{k} x^{k}$
The polynomial oscillates wildly in places, in order to both interpolate the data and to have all derivatives wrt $x$ continuous

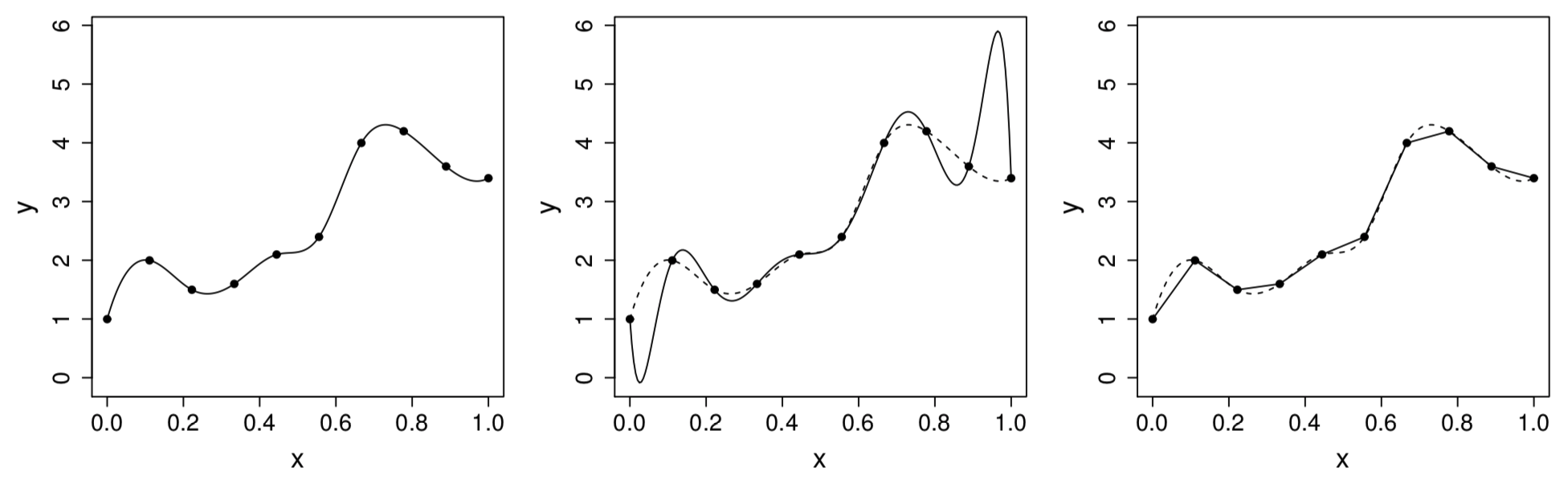
Figure 1: Left: the target function $f (x)$ . Middle: polynomial interpolation. Right: piecewise linear interpolant

Piecewise linear basis

Suppose there are $k$ knots $x_{1}^{*} < x_{2}^{*} < \dots < x_{k}^{*}$
The tent function representation of piecewise linear basis is
- For $j = 2, \dots, k - 1$ , $b_{j} (x) = {\begin{cases} \frac{x - x_{j - 1}^{*}}{x_{j}^{*} - x_{j - 1}^{*}}, & if x_{j - 1}^{*} < x \leq x_{j}^{*} \\ \frac{x_{j + 1}^{*} - x}{x_{j + 1}^{*} - x_{j}^{*}}, & if x_{j}^{*} < x \leq x_{j + 1}^{*} \\ 0, & otherwise \end{cases}$
- For the two basis functions on the edge $\begin{aligned} b_{1} (x) & = {\begin{cases} \frac{x_{2}^{*} - x}{x_{2}^{*} - x_{1}^{*}}, & if x \leq x_{2}^{*} \\ 0, & otherwise \end{cases} \\ b_{k} (x) & = {\begin{cases} \frac{x - x_{k - 1}^{*}}{x_{k}^{*} - x_{k - 1}^{*}}, & x > x_{k - 1}^{*} \\ 0, & otherwise \end{cases} \end{aligned}$

Visualization of tent function basis

$b_{j} (x)$ is zero everywhere, except over the interval between the knots immediately to either side of $x_{j}^{*}$
$b_{j} (x)$ increases linear from $0$ at $x_{j - 1}^{*}$ to 1 at $x_{j}^{*}$ , and then decreases linearly to $0$ at $x_{j + 1}^{*}$

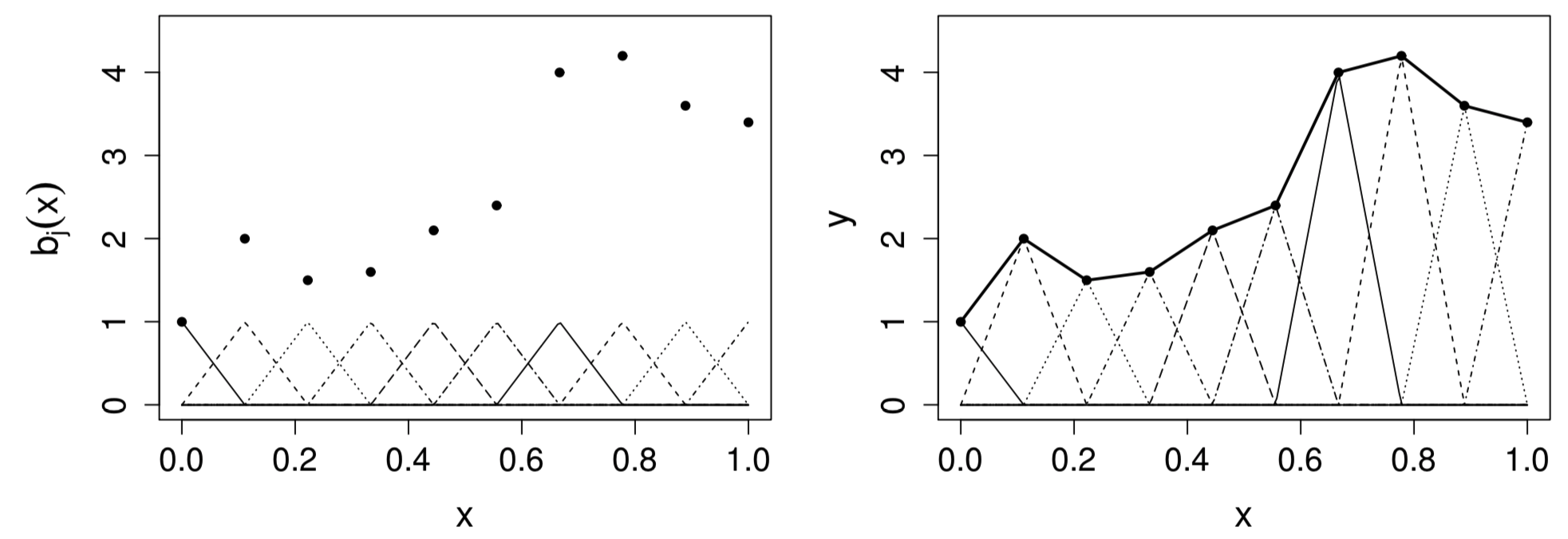
Left: tent function basis, for interpolating the data shown as black dots. Right: the basis functiosn are each multiplied by a coefficient, before being summed

Figure 2: Left: tent function basis, for interpolating the data shown as black dots. Right: the basis functiosn are each multiplied by a coefficient, before being summed

Penalty to control wiggliness

Control smoothness by penalizing wiggliness

To choose the degree of smoothness, rather than selecting the number of knots $k$ , we can use a relatively large $k$ , but control the model’s smoothness by adding a “wiggliness” penalty
- Note that a model based on $k - 1$ evenly spaced knots will not be nested within a model based on $k$ evenly spaced knots
Penalized likelihood function for piecewise linear basis: $‖ y - X β ‖^{2} + λ \sum_{j = 2}^{k - 1} {[f (x_{j - 1}^{*}) - 2 f (x_{j}^{*}) + f (x_{j + 1}^{*})]}^{2}$
- Wiggliness is measured as a sum of squared second differences of the function at the knots
- This crudely approximates the integrated squared second derivative penalty used in cubic spline smoothing
- $λ$ is called the smoothing parameter

Simplify the penalized likelihood

For the tent function basis, $β_{j} = f (x_{j}^{*})$
Therefore, the penalty can be expressed as a quadratic form $\sum_{j = 2}^{k - 1} (β_{j - 1} - 2 β_{j} + β_{j + 1})^{2} = β^{T} D^{T} D β = β^{T} S β$
- The $(k - 2) \times k$ matrix $D$ is $D = [\begin{array}{ccccccc} 1 & - 2 & 1 & 0 & . & . & . \\ 0 & 1 & - 2 & 1 & 0 & . & . \\ 0 & 0 & 1 & - 2 & 1 & 0 & . \\ . & . & . & . & . & . & . \\ . & . & . & . & . & . & . \end{array}]$
- $S = D^{T} D$ is a square matrix

Solution of the penalized regression

To minimize the penalized likelihood $\begin{aligned} \hat{β} & = \arg min_{β} ‖ y - X β ‖^{2} + λ β^{T} S β \\ = (X^{T} X + λ S)^{- 1} X^{T} y \end{aligned}$
The hat matrix (also called influence matrix) $A$ is thus $A = X (X^{T} X + λ S)^{- 1} X^{T}$ and the fitted expectation is $\hat{μ} = A y$
For practical computation, we can introduce imaginary data to re-formulate the penalized least square problem to be a regular least square problem $‖ y - X β ‖^{2} + λ β^{T} S β = {‖ [\begin{matrix} y \\ 0 \end{matrix}] - [\begin{matrix} X \\ \sqrt{λ} D \end{matrix}] β ‖}^{2}$

Hyper-parameter tuning

Between the two hyper-parameters: number of knots $k$ and the smoothing parameter $λ$ , the choice of $λ$ plays the crucial role
We can always use a $k$ large enough, more flexible then we expect to need to represent $f (x)$
In mgcv package, the default choice is $k = 20$ , and knots are evenly spread out over the range of observed data

Choose $λ$ by leave-one-out cross validation

Under linear regression, to compute leave-one-out cross validation error (called the ordinary cross validation score), we only need to fit the full model once $V_{o} = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{f}}_{i}^{[- i]})}^{2} = \frac{1}{n} \sum_{i = 1}^{n} \frac{{(y_{i} - {\hat{f}}_{i})}^{2}}{(1 - A_{i i})^{2}}$
- ${\hat{f}}_{i}^{[- i]}$ is the model fitted to all data except $y_{i}$
- ${\hat{f}}_{i}$ is the model fitted to all data, and $A_{i i}$ is the $i$ th diagonal entry of the corresponding hat matrix
In practice, $A_{i i}$ are often replaced by their mean $tr (A) / n$ . This results in the generalized cross validation score (GCV) $V_{g} = \frac{n \sum_{i = 1}^{n} {(y_{i} - {\hat{f}}_{i})}^{2}}{{[n - tr (A)]}^{2}}$

From the Bayesian perspective

The wiggliness penalty can be viewed as a normal prior distribution on $β$ $β \sim N (0, σ^{2} \frac{S^{-}}{λ})$
- Because $S$ is rank deficient, the prior covariance is proportional to the pseudo-inverse $S^{-}$
The posterior of $β$ is still normal $β ∣ y \sim N (\hat{β}, (X^{T} X + λ S)^{- 1} σ^{2})$
Given the model this extra structure opens up the possibility of estimating $σ^{2}$ and $λ$ using marginal likelihood maximization or REML (aka empirical Bayes)

Additive Models

A simple additive model with two univariate functions

Let’s consider a simple additive model $y_{i} = α + f_{1} (x_{i}) + f_{2} (v_{i}) + ϵ_{i}, ϵ_{i} \overset{iid}{\sim} N (0, σ^{2})$
The assumption of additive effects is a fairly strong one
The model now has an identifiability problem: $f_{1}$ and $f_{2}$ are each only estimable to within an additive constant
- Due to the identifiability issue, we need to use penalized regression splines

Piecewise linear regression representation

Basis representation of $f_{1} ()$ and $f_{2} ()$ $\begin{aligned} f_{1} (x) = \sum_{j = 1}^{k_{1}} b_{j} (x) δ_{j} \\ f_{2} (v) = \sum_{j = 1}^{k_{2}} B_{j} (v) γ_{j} \end{aligned}$
- The basis functions $b_{j} ()$ and $B_{j} ()$ are tent functions, with evenly spaced knots $x_{j}^{*}$ and $v_{j}^{*}$ , respectively
Matrix representations $\begin{aligned} f_{1} & = [f_{1} (x_{1}), \dots, f_{1} (x_{n})]^{T} = X_{1} δ, [X_{1}]_{i, j} = b_{j} (x_{i}) \\ f_{2} & = [f_{2} (v_{1}), \dots, f_{2} (v_{n})]^{T} = X_{2} γ, [X_{2}]_{i, j} = B_{j} (x_{i}) \end{aligned}$

Sum-to-zero constrains to resolve identifiability issues

We assume $\sum_{i = 1}^{n} f_{1} (x_{i}) = 0 ⟺ 1^{T} f_{1} = 0$ This is equivalent to $1^{T} X_{1} δ = 0$ for all $δ$ , which implies $1^{T} X_{1} = 0$
To achieve this condition, we can center the column of $X_{1}$ ${\tilde{X}}_{1} = X_{1} - 1 \frac{1^{T} X_{1}}{n}, {\tilde{f}}_{1} = {\tilde{X}}_{1} δ$
Column centering reduces the rank of ${\tilde{X}}_{1}$ to $k_{1} - 1$ , so that only $k_{1} - 1$ elements of the $k_{1}$ vector $δ$ can be uniquely estimated
A simple identifiability constraint:
- Set a single element of $δ$ to zero
- And delete the corresponding column of ${\tilde{X}}_{1}$ and $D$
For notation simplicity, in what follows the tildes will be dropped, and we assume that the $X_{j}$ , $D_{j}$ are the constrained versions

Penalized piecewise regression additive model

We rewrite the penalized regression as $y = X β + ϵ$ where $X = (1, X_{1}, X_{2})$ and $β^{T} = (α, δ^{T}, γ^{T})$
Wiggliness penalties $\begin{aligned} δ^{T} D_{1}^{T} D_{1} δ & = δ^{T} {\bar{S}}_{1} δ = β^{T} S_{1} β, S_{1} = [\begin{array}{ccc} 0 & 0 & 0 \\ 0 & {\bar{S}}_{1} & 0 \\ 0 & 0 & 0 \end{array}] \\ γ^{T} D_{2}^{T} D_{2} γ & = γ^{T} {\bar{S}}_{2} γ = β^{T} S_{2} β, \end{aligned}$

Fitting additive models by penalized least squares

Penalized least squares objective function $‖ y - X β ‖^{2} + λ_{1} β^{T} S_{1} β + λ_{2} β^{T} S_{2} β$
Coefficient estimator $\hat{β} = {(X^{T} X + λ_{1} S_{1} + λ_{2} S_{2})}^{- 1} X^{T} y$
Hat matrix $A = X {(X^{T} X + λ_{1} S_{1} + λ_{2} S_{2})}^{- 1} X^{T}$
Conditional posterior distribution $β ∣ y \sim N (\hat{β}, {\hat{V}}_{β}), {\hat{V}}_{β} = {(X^{T} X + λ_{1} S_{1} + λ_{2} S_{2})}^{- 1} {\hat{σ}}^{2}$

Choosing two smoothing parameters

Since we now have two smoothing parameters $λ_{1}, λ_{2}$ , grid searching for the GCV optimal values starts to become inefficient
Instead, R function optim can be used to minimize the GCV score
We can use log smoothing parameters for optimization to ensure that estimated smoothing parameters are non-negative

Generalized Additive Models

Generalized additive models

Generalized additive models (GAMs): additive models $+$ GLM $g (μ_{i}) = α + f_{1} (x_{i}) + f_{2} (v_{i}) + ϵ_{i}$
Penalized iterative least squares (PIRLS) algorithm: iterate the following steps to convergence

Given the current $\hat{η}$ and $\hat{μ}$ , compute $w_{i} = \frac{1}{V ({\hat{μ}}_{i}) g^{'} ({\hat{μ}}_{i})^{2}}, z_{i} = g^{'} ({\hat{μ}}_{i}) (y_{i} - {\hat{μ}}_{i}) + {\hat{η}}_{i}$
Let $W = diag (w_{i})$ , we obtain the new $\hat{β}$ by minimizing $‖ \sqrt{W} z - \sqrt{W} X β ‖^{2} + λ_{1} β^{T} S_{1} β + λ_{2} β^{T} S_{2} β$

Introducing Package `mgcv`

Introducing package `mgcv`

Main function: gam(), very much like the glm() function
Smooth terms: s() for univariate functions and te() for tensors
A gamma regression example $\log (E [{\tt Volume}_{i}]) = f_{1} ({\tt Height}_{i}) + f_{2} ({\tt Girth}_{i}), {\tt Volume}_{i} \sim Gamma$

library(mgcv) ## load the package data(trees)
ct1 <- gam(Volume ~ s(Height) + s(Girth),
           family=Gamma(link=log),data=trees)

By default, the degree of smoothness of the $f_{j}$ is estimated by GCV

summary(ct1)

## 
## Family: Gamma 
## Link function: log 
## 
## Formula:
## Volume ~ s(Height) + s(Girth)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.27570    0.01492   219.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##             edf Ref.df      F  p-value    
## s(Height) 1.000  1.000  31.32 7.07e-06 ***
## s(Girth)  2.422  3.044 219.28  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.973   Deviance explained = 97.8%
## GCV = 0.0080824  Scale est. = 0.006899  n = 31

Parital residuals plots

Pearson residuals added to the estimated smooth terms ${\hat{ϵ}}_{1 i}^{partial} = f_{1} ({\tt Height}_{i}) + {\hat{ϵ}}_{i}^{p}$

par(mfrow = c(1, 2))
plot(ct1,residuals=TRUE)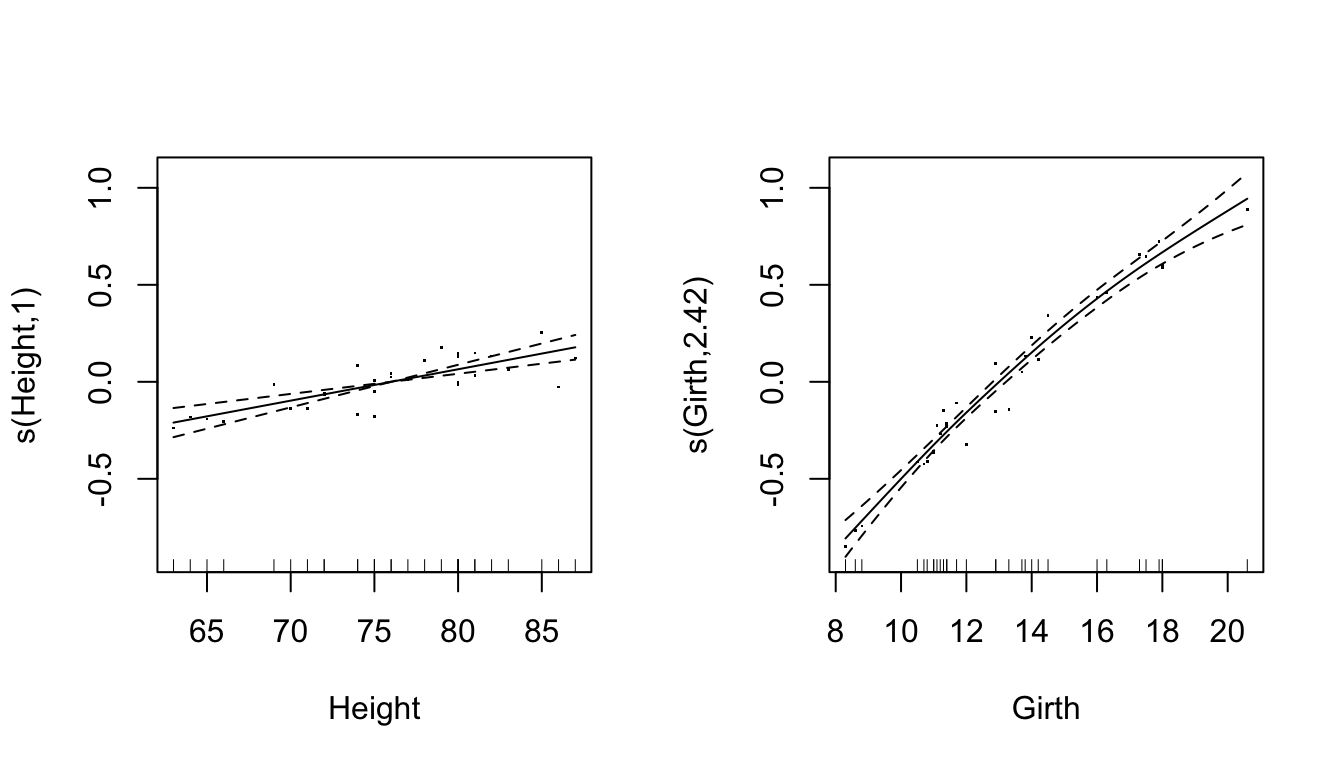

* The number in the $y$ -axis label: effective degrees of freedom

Finer control of `gam()`: choice of basis functions

Default: thin plat regression splines
- It has some appealing properties, but can be somewhat computationally costly for large dataset
We can select penalized cubic regression spline by using

s(..., bs = "cr")

We can change the dimension $k$ of the basis
- The actual effective degrees of freedom for each term is usually estimated from the data by GCV or another smoothness selection criterion
- The upper bound on this estimate is $k - 1$ , minus one due to identifiability constraint on each smooth term

s(..., bs = "cr", k = 20)

Finer control of `gam()`: the `gamma` parameter

GCV is known to have some tendency to overfitting
Inside the gam() function, the argument gamma can increase the amount of smoothing
- The default value for gamma is 1
- We can use a higher value to avoid overfitting, gamma = 1.5, without compromising model fit

References

Wood, Simon N. (2017), Generalized Additive Models: An Introduction with R. Chapman and Hall/CRC

Book Notes: Generalized Additive Models -- Ch4 Introducing GAMs