Book Notes: Generalized Additive Models -- Ch4 Introducing GAMs

For the pdf slides, click here

Introduction of GAM

  • In general the GAM model has a following structure \[ g(\mu_i) = \mathbf{A}_i \boldsymbol\theta + f_1 (x_{1i}) + f_2 (x_{2i}) + f_3 (x_{3i}, x_{4i}) + \cdots \]

    • \(Y_i\) follows some exponential family distribution: \(Y_i \sim EF(\mu_i, \phi)\)
    • \(\mu_i = E(Y_i)\)
    • \(\mathbf{A}_i\) is a row of the model matrix, and \(\boldsymbol\theta\) is the corresponding parameter vector
    • \(f_j\) are smooth functions of the covariates \(x_k\)
  • This chapter
    • Illustrates GAMs by basis expansions, each with a penalty controlling function smoothness
    • Estimates GAMs by penalized regression methods

  • Takeaway: technically GAMs are simply GLM estimated subject to smoothing penalties

Univariate Smoothing

Piecewise linear basis: tent functions

Representing a function with basis expansions

  • Let’s consider a model containing one function of one covariate \[ y_i = f(x_i) + \epsilon_i, \quad \epsilon_i \stackrel{\text{iid}}{\sim} \text{N}(0, \sigma^2) \]

  • If \(b_j(x)\) is the \(j\)th basis function, then \(f\) is assumed to have a representation \[ f(x) = \sum_{j=1}^k b_j(x)\beta_j \] with some unknown parameters \(\beta_j\)

    • This is clearly a linear model

The problem with polynomials

  • A \(k\)th order polynomial is \[ f(x) = \beta_0 + \sum_{j=1}^k \beta_k x^k \]

  • The polynomial oscillates wildly in places, in order to both interpolate the data and to have all derivatives wrt \(x\) continuous

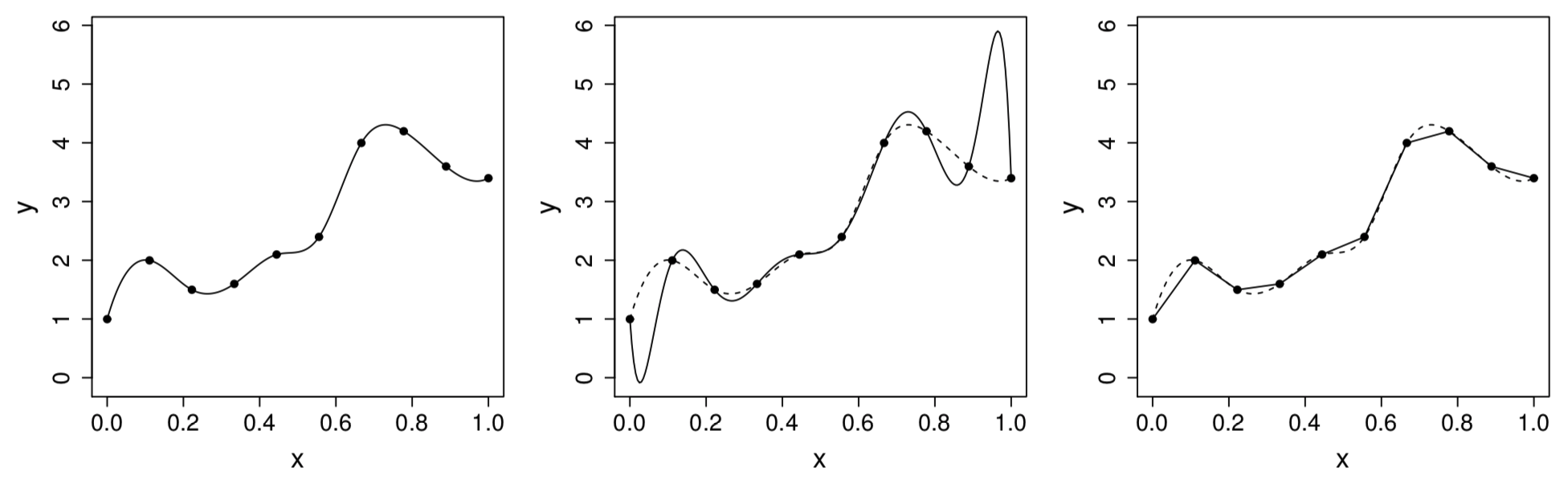
Left: the target function $f(x)$. Middle: polynomial interpolation. Right: piecewise linear interpolant

Figure 1: Left: the target function \(f(x)\). Middle: polynomial interpolation. Right: piecewise linear interpolant

Piecewise linear basis

  • Suppose there are \(k\) knots \(x_1^* < x_2^* < \cdots <x_k^*\)

  • The tent function representation of piecewise linear basis is

    • For \(j = 2, \ldots, k-1\), \[ b_j(x) = \begin{cases} \frac{x - x_{j-1}^*}{x_j^* - x_{j-1}^*}, & \text{if } x_{j-1}^* < x \leq x_j^*\\ \frac{x_{j+1}^* - x}{x_{j+1}^* - x_j^*}, & \text{if } x_j^* < x \leq x_{j+1}^*\\ 0, & \text{otherwise} \end{cases} \]
    • For the two basis functions on the edge \[\begin{align*} b_1(x) & = \begin{cases} \frac{x_2^* - x}{x_2^* - x_1^*}, & \text{if } x \leq x_2^*\\ 0, & \text{otherwise} \end{cases}\\ b_k(x) & = \begin{cases} \frac{x - x_{k-1}^*}{x_k^* - x_{k-1}^*}, & x > x_{k-1}^*\\ 0, & \text{otherwise} \end{cases} \end{align*}\]

Visualization of tent function basis

  • \(b_j(x)\) is zero everywhere, except over the interval between the knots immediately to either side of \(x_j^*\)

  • \(b_j(x)\) increases linear from \(0\) at \(x_{j-1}^*\) to 1 at \(x_j^*\), and then decreases linearly to \(0\) at \(x_{j+1}^*\)

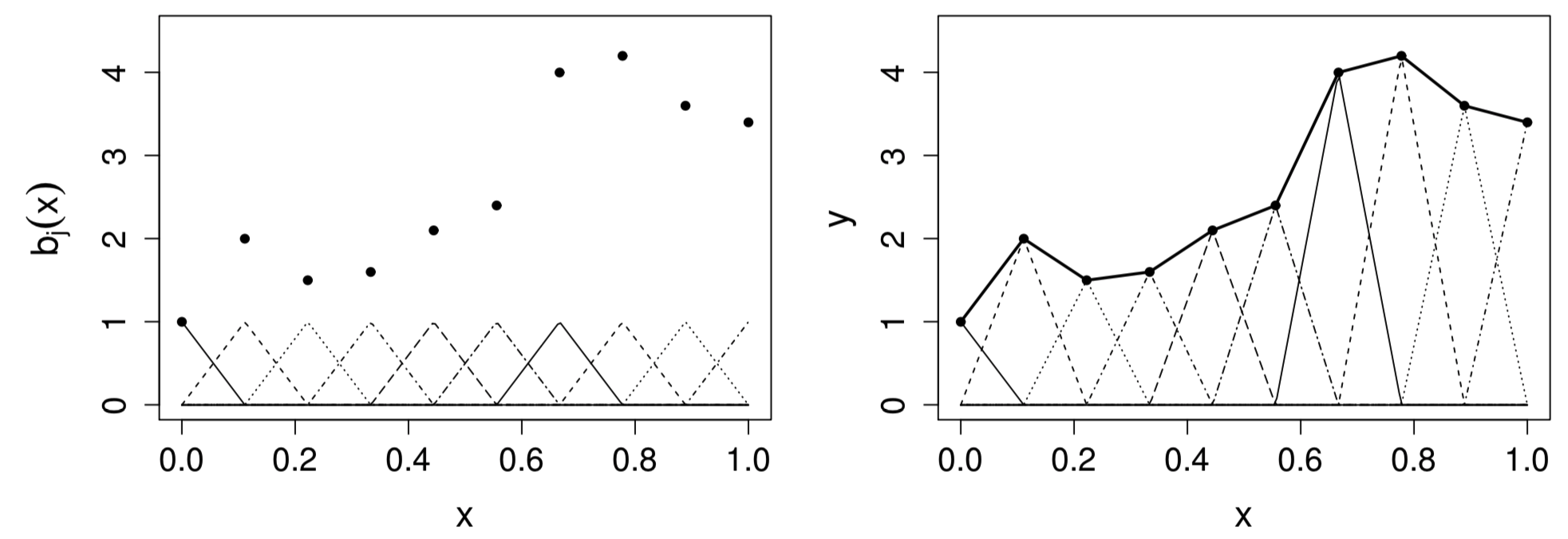
Left: tent function basis, for interpolating the data shown as black dots. Right: the basis functiosn are each multiplied by a coefficient, before being summed

Figure 2: Left: tent function basis, for interpolating the data shown as black dots. Right: the basis functiosn are each multiplied by a coefficient, before being summed

Penalty to control wiggliness

Control smoothness by penalizing wiggliness

  • To choose the degree of smoothness, rather than selecting the number of knots \(k\), we can use a relatively large \(k\), but control the model’s smoothness by adding a “wiggliness” penalty

    • Note that a model based on \(k-1\) evenly spaced knots will not be nested within a model based on \(k\) evenly spaced knots

  • Penalized likelihood function for piecewise linear basis: \[ \|\mathbf{y} - \mathbf{X}\boldsymbol\beta\|^2 + \lambda \sum_{j=2}^{k-1} \left[ f(x_{j-1}^*) - 2f(x_j^*) + f(x_{j+1}^*) \right]^2 \]

    • Wiggliness is measured as a sum of squared second differences of the function at the knots
    • This crudely approximates the integrated squared second derivative penalty used in cubic spline smoothing
    • \(\lambda\) is called the smoothing parameter

Simplify the penalized likelihood

  • For the tent function basis, \(\beta_j = f(x_j^*)\)

  • Therefore, the penalty can be expressed as a quadratic form \[ \sum_{j=2}^{k-1} (\beta_{j-1} - 2 \beta_j + \beta_{j+1})^2 = \boldsymbol\beta^T \mathbf{D}^T\mathbf{D}\boldsymbol\beta = \boldsymbol\beta^T \mathbf{S}\boldsymbol\beta \]

    • The \((k-2)\times k\) matrix \(\mathbf{D}\) is \[ \mathbf{D} = \left[ \begin{array}{ccccccc} 1 & -2 & 1 & 0 & . & . & . \\ 0 & 1 & -2 & 1 & 0 & . & . \\ 0 & 0 & 1 & -2 & 1 & 0 & . \\ . & . & . & . & . & . & . \\ . & . & . & . & . & . & . \\ \end{array} \right] \]
    • \(\mathbf{S} = \mathbf{D}^T\mathbf{D}\) is a square matrix

Solution of the penalized regression

  • To minimize the penalized likelihood \[\begin{align*} \hat{\boldsymbol\beta} &= \arg\min_{\boldsymbol\beta}~ \|\mathbf{y} - \mathbf{X}\boldsymbol\beta \|^2 + \lambda \boldsymbol\beta^T \mathbf{S} \boldsymbol\beta\\ &= (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{S})^{-1} \mathbf{X}^T\mathbf{y} \end{align*}\]

  • The hat matrix (also called influence matrix) \(\mathbf{A}\) is thus \[ \mathbf{A} = \mathbf{X} (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{S})^{-1} \mathbf{X}^T \] and the fitted expectation is \(\hat{\boldsymbol\mu} = \mathbf{A} \mathbf{y}\)

  • For practical computation, we can introduce imaginary data to re-formulate the penalized least square problem to be a regular least square problem \[ \|\mathbf{y} - \mathbf{X}\boldsymbol\beta \|^2 + \lambda \boldsymbol\beta^T \mathbf{S} \boldsymbol\beta = \left\|\left[ \begin{array}{c} \mathbf{y}\\ \mathbf{0} \end{array} \right] - \left[ \begin{array}{c} \mathbf{X}\\ \sqrt{\lambda}\mathbf{D} \end{array} \right] \boldsymbol\beta \right\|^2 \]

Hyper-parameter tuning

  • Between the two hyper-parameters: number of knots \(k\) and the smoothing parameter \(\lambda\), the choice of \(\lambda\) plays the crucial role

  • We can always use a \(k\) large enough, more flexible then we expect to need to represent \(f(x)\)

  • In mgcv package, the default choice is \(k = 20\), and knots are evenly spread out over the range of observed data

Choose \(\lambda\) by leave-one-out cross validation

  • Under linear regression, to compute leave-one-out cross validation error (called the ordinary cross validation score), we only need to fit the full model once \[ \mathcal{V}_o = \frac{1}{n} \sum_{i=1}^n \left(y_i - \hat{f}^{[-i]}_i \right)^2 = \frac{1}{n} \sum_{i=1}^n \frac{\left(y_i - \hat{f}_i\right)^2}{(1 - A_{ii})^2} \]

    • \(\hat{f}^{[-i]}_i\) is the model fitted to all data except \(y_i\)
    • \(\hat{f}_i\) is the model fitted to all data, and \(A_{ii}\) is the \(i\)th diagonal entry of the corresponding hat matrix

  • In practice, \(A_{ii}\) are often replaced by their mean \(\text{tr}(\mathbf{A})/n\). This results in the generalized cross validation score (GCV) \[ \mathcal{V}_g = \frac{n \sum_{i=1}^n \left(y_i - \hat{f}_i\right)^2}{\left[n - \text{tr}(\mathbf{A}) \right]^2} \]

From the Bayesian perspective

  • The wiggliness penalty can be viewed as a normal prior distribution on \(\boldsymbol\beta\) \[ \boldsymbol\beta \sim \text{N}\left(\mathbf{0}, \sigma^2 \frac{\mathbf{S}^{-}}{\lambda} \right) \]

    • Because \(\mathbf{S}\) is rank deficient, the prior covariance is proportional to the pseudo-inverse \(\mathbf{S}^{-}\)

  • The posterior of \(\boldsymbol\beta\) is still normal \[ \boldsymbol\beta \mid \mathbf{y} \sim \text{N}\left(\hat{\boldsymbol\beta}, (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{S})^{-1} \sigma^2 \right) \]

  • Given the model this extra structure opens up the possibility of estimating \(\sigma^2\) and \(\lambda\) using marginal likelihood maximization or REML (aka empirical Bayes)

Additive Models

A simple additive model with two univariate functions

  • Let’s consider a simple additive model \[ y_i = \alpha + f_1(x_i) + f_2(v_i) + \epsilon_i, \quad \epsilon_i \stackrel{\text{iid}}{\sim} \text{N}(0, \sigma^2) \]

  • The assumption of additive effects is a fairly strong one

  • The model now has an identifiability problem: \(f_1\) and \(f_2\) are each only estimable to within an additive constant

    • Due to the identifiability issue, we need to use penalized regression splines

Piecewise linear regression representation

  • Basis representation of \(f_1()\) and \(f_2()\) \[\begin{align*} f_1(x) = \sum_{j=1}^{k_1} b_j(x) \delta_j\\ f_2(v) = \sum_{j=1}^{k_2} \mathcal{B}_j(v) \gamma_j \end{align*}\]

    • The basis functions \(b_j()\) and \(\mathcal{B}_j()\) are tent functions, with evenly spaced knots \(x_j^*\) and \(v_j^*\), respectively

  • Matrix representations \[\begin{align*} \mathbf{f}_1 & = [f_1(x_1), \ldots, f_1(x_n)]^T = \mathbf{X}_1 \boldsymbol\delta, \quad [\mathbf{X}_1]_{i,j} = b_j (x_i)\\ \mathbf{f}_2 & = [f_2(v_1), \ldots, f_2(v_n)]^T = \mathbf{X}_2 \boldsymbol\gamma, \quad [\mathbf{X}_2]_{i,j} = \mathcal{B}_j (x_i) \end{align*}\]

Sum-to-zero constrains to resolve identifiability issues

  • We assume \[ \sum_{i=1}^n f_1(x_i) = 0 \Longleftrightarrow \mathbf{1}^T \mathbf{f}_1 = 0 \] This is equivalent to \(\mathbf{1}^T \mathbf{X}_1 \boldsymbol\delta = 0\) for all \(\boldsymbol\delta\), which implies \(\mathbf{1}^T \mathbf{X}_1 = \mathbf{0}\)

  • To achieve this condition, we can center the column of \(\mathbf{X}_1\) \[ \tilde{\mathbf{X}}_1 = \mathbf{X}_1 - \mathbf{1}~\frac{\mathbf{1}^T\mathbf{X}_1}{n}, \quad \tilde{\mathbf{f}}_1 = \tilde{\mathbf{X}}_1 \boldsymbol\delta \]

  • Column centering reduces the rank of \(\tilde{\mathbf{X}}_1\) to \(k_1 -1\), so that only \(k_1-1\) elements of the \(k_1\) vector \(\boldsymbol\delta\) can be uniquely estimated

  • A simple identifiability constraint:
    • Set a single element of \(\boldsymbol\delta\) to zero
    • And delete the corresponding column of \(\tilde{\mathbf{X}}_1\) and \(\mathbf{D}\)

  • For notation simplicity, in what follows the tildes will be dropped, and we assume that the \(\mathbf{X}_j\), \(\mathbf{D}_j\) are the constrained versions

Penalized piecewise regression additive model

  • We rewrite the penalized regression as \[ \mathbf{y} = \mathbf{X}\boldsymbol\beta + \boldsymbol\epsilon \] where \(X = (\mathbf{1}, \mathbf{X}_1, \mathbf{X}_2)\) and \(\boldsymbol\beta^T = (\alpha, \boldsymbol\delta^T, \boldsymbol\gamma^T)\)

  • Wiggliness penalties \[\begin{align*} \boldsymbol\delta^T \mathbf{D}_1^T \mathbf{D}_1 \boldsymbol\delta & = \boldsymbol\delta^T \bar{\mathbf{S}}_1 \boldsymbol\delta = \boldsymbol\beta^T \mathbf{S}_1 \boldsymbol\beta, \quad \mathbf{S}_1 = \left[ \begin{array}{ccc} 0 & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \bar{\mathbf{S}}_1 & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & \mathbf{0} \end{array} \right]\\ \boldsymbol\gamma^T \mathbf{D}_2^T \mathbf{D}_2 \boldsymbol\gamma & = \boldsymbol\gamma^T \bar{\mathbf{S}}_2 \boldsymbol\gamma = \boldsymbol\beta^T \mathbf{S}_2 \boldsymbol\beta, \end{align*}\]

Fitting additive models by penalized least squares

  • Penalized least squares objective function \[ \|\mathbf{y} - \mathbf{X} \boldsymbol\beta \|^2+ \lambda_1 \boldsymbol\beta^T \mathbf{S}_1 \boldsymbol\beta+ \lambda_2 \boldsymbol\beta^T \mathbf{S}_2 \boldsymbol\beta \]

  • Coefficient estimator \[ \hat{\boldsymbol\beta} = \left(\mathbf{X}^T\mathbf{X} + \lambda_1\mathbf{S}_1 + \lambda_2\mathbf{S}_2 \right)^{-1}\mathbf{X}^T\mathbf{y} \]

  • Hat matrix \[ \mathbf{A} = \mathbf{X}\left(\mathbf{X}^T\mathbf{X} + \lambda_1\mathbf{S}_1 + \lambda_2\mathbf{S}_2 \right)^{-1}\mathbf{X}^T \]

  • Conditional posterior distribution \[ \boldsymbol\beta \mid \mathbf{y} \sim \text{N}\left(\hat{\boldsymbol\beta}, \hat{\mathbf{V}}_{\boldsymbol\beta}\right), \quad \hat{\mathbf{V}}_{\boldsymbol\beta} = \left(\mathbf{X}^T\mathbf{X} + \lambda_1\mathbf{S}_1 + \lambda_2\mathbf{S}_2 \right)^{-1} \hat{\sigma}^2 \]

Choosing two smoothing parameters

  • Since we now have two smoothing parameters \(\lambda_1, \lambda_2\), grid searching for the GCV optimal values starts to become inefficient

  • Instead, R function optim can be used to minimize the GCV score

  • We can use log smoothing parameters for optimization to ensure that estimated smoothing parameters are non-negative

Generalized Additive Models

Generalized additive models

  • Generalized additive models (GAMs): additive models \(+\) GLM \[ g(\mu_i) = \alpha + f_1(x_i) + f_2(v_i) + \epsilon_i \]

  • Penalized iterative least squares (PIRLS) algorithm: iterate the following steps to convergence

  1. Given the current \(\hat{\boldsymbol\eta}\) and \(\hat{\boldsymbol\mu}\), compute \[ w_i = \frac{1}{V(\hat{\mu}_i) g^{\prime}(\hat{\mu}_i)^2}, \quad z_i = g^{\prime}(\hat{\mu}_i)(y_i - \hat{\mu}_i) + \hat{\eta}_i \]

  2. Let \(\mathbf{W} = \text{diag}(w_i)\), we obtain the new \(\hat{\boldsymbol\beta}\) by minimizing \[ \|\sqrt{\mathbf{W}} \mathbf{z} - \sqrt{\mathbf{W}} \mathbf{X}\boldsymbol\beta\|^2 + \lambda_1 \boldsymbol\beta^T \mathbf{S}_1 \boldsymbol\beta + \lambda_2 \boldsymbol\beta^T \mathbf{S}_2 \boldsymbol\beta \]

Introducing Package mgcv

Introducing package mgcv

  • Main function: gam(), very much like the glm() function

  • Smooth terms: s() for univariate functions and te() for tensors

  • A gamma regression example \[ \log\left(E\left[\text{\tt Volume}_i \right]\right) = f_1(\text{\tt Height}_i) + f_2(\text{\tt Girth}_i), \quad \text{\tt Volume}_i \sim \text{Gamma} \]

library(mgcv) ## load the package data(trees)
ct1 <- gam(Volume ~ s(Height) + s(Girth),
           family=Gamma(link=log),data=trees)
  • By default, the degree of smoothness of the \(f_j\) is estimated by GCV

summary(ct1)
## 
## Family: Gamma 
## Link function: log 
## 
## Formula:
## Volume ~ s(Height) + s(Girth)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.27570    0.01492   219.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##             edf Ref.df      F  p-value    
## s(Height) 1.000  1.000  31.32 7.07e-06 ***
## s(Girth)  2.422  3.044 219.28  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.973   Deviance explained = 97.8%
## GCV = 0.0080824  Scale est. = 0.006899  n = 31

Parital residuals plots

  • Pearson residuals added to the estimated smooth terms \[ \hat{\epsilon}_{1i}^{\text{partial}} = f_1(\text{\tt Height}_i) + \hat{\epsilon}_{i}^{p} \]
par(mfrow = c(1, 2))
plot(ct1,residuals=TRUE)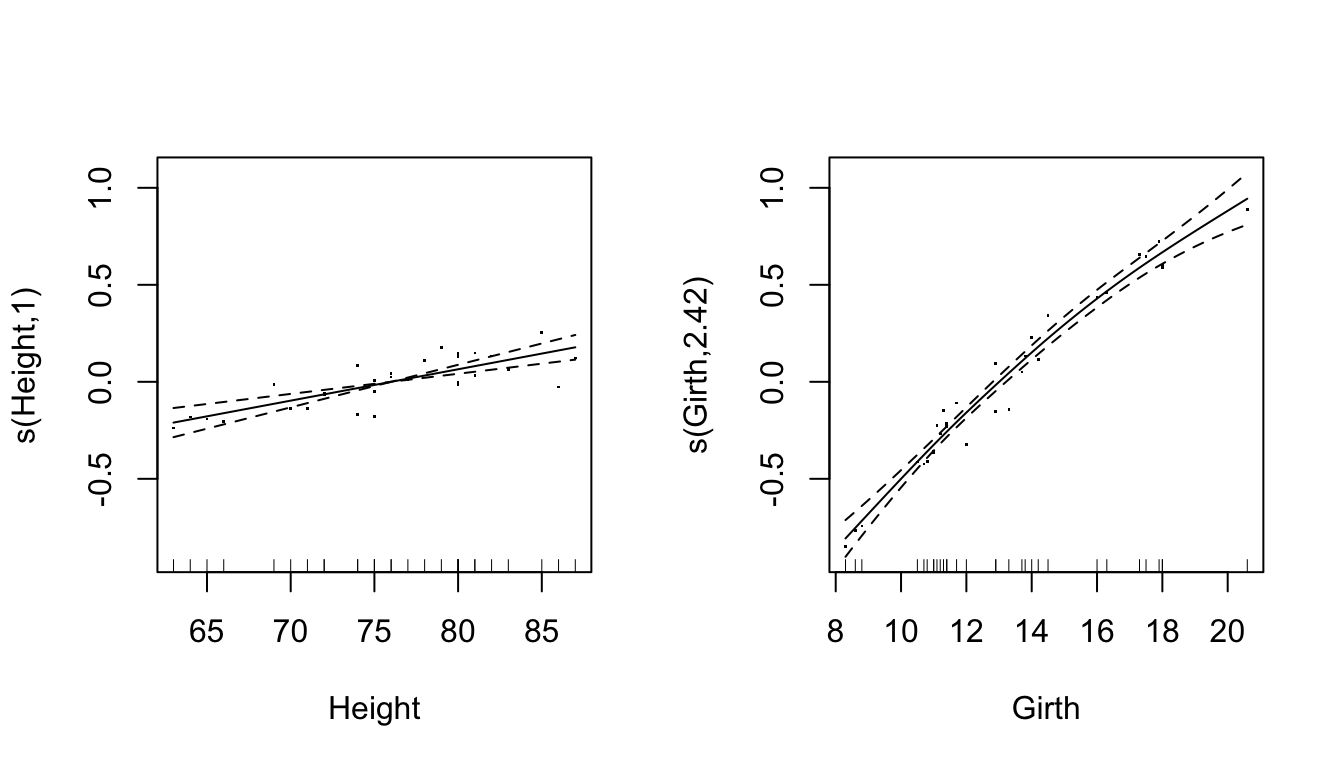

* The number in the \(y\)-axis label: effective degrees of freedom

Finer control of gam(): choice of basis functions

  • Default: thin plat regression splines

    • It has some appealing properties, but can be somewhat computationally costly for large dataset

  • We can select penalized cubic regression spline by using

s(..., bs = "cr")

  • We can change the dimension \(k\) of the basis

    • The actual effective degrees of freedom for each term is usually estimated from the data by GCV or another smoothness selection criterion
    • The upper bound on this estimate is \(k-1\), minus one due to identifiability constraint on each smooth term
s(..., bs = "cr", k = 20)

Finer control of gam(): the gamma parameter

  • GCV is known to have some tendency to overfitting

  • Inside the gam() function, the argument gamma can increase the amount of smoothing

    • The default value for gamma is 1
    • We can use a higher value to avoid overfitting, gamma = 1.5, without compromising model fit

References

  • Wood, Simon N. (2017), Generalized Additive Models: An Introduction with R. Chapman and Hall/CRC