CNN overview for NLP

• CBOW assigns the following two sentences the same representations

  • “it was not good, it was actually quite bad”
  • “it was not bad, it was actually quite good”

• Looking at ngrams is much more informative than looking at a bag-of-words

• This chapter introduces the convolution-and-pooling (also called convolutional neural networks, or CNNs), which is tailored to this modeling problem

Benefits of CNN for NLP

• CNNs will identify ngrams that are predictive for the task at hand, without the need to pre-specify an embedding vector for each possible ngram

• CNNs also allows to share predictive behavior between ngrams that share similar components, even if the exact ngrams was never seen at test time

• Example paper: link

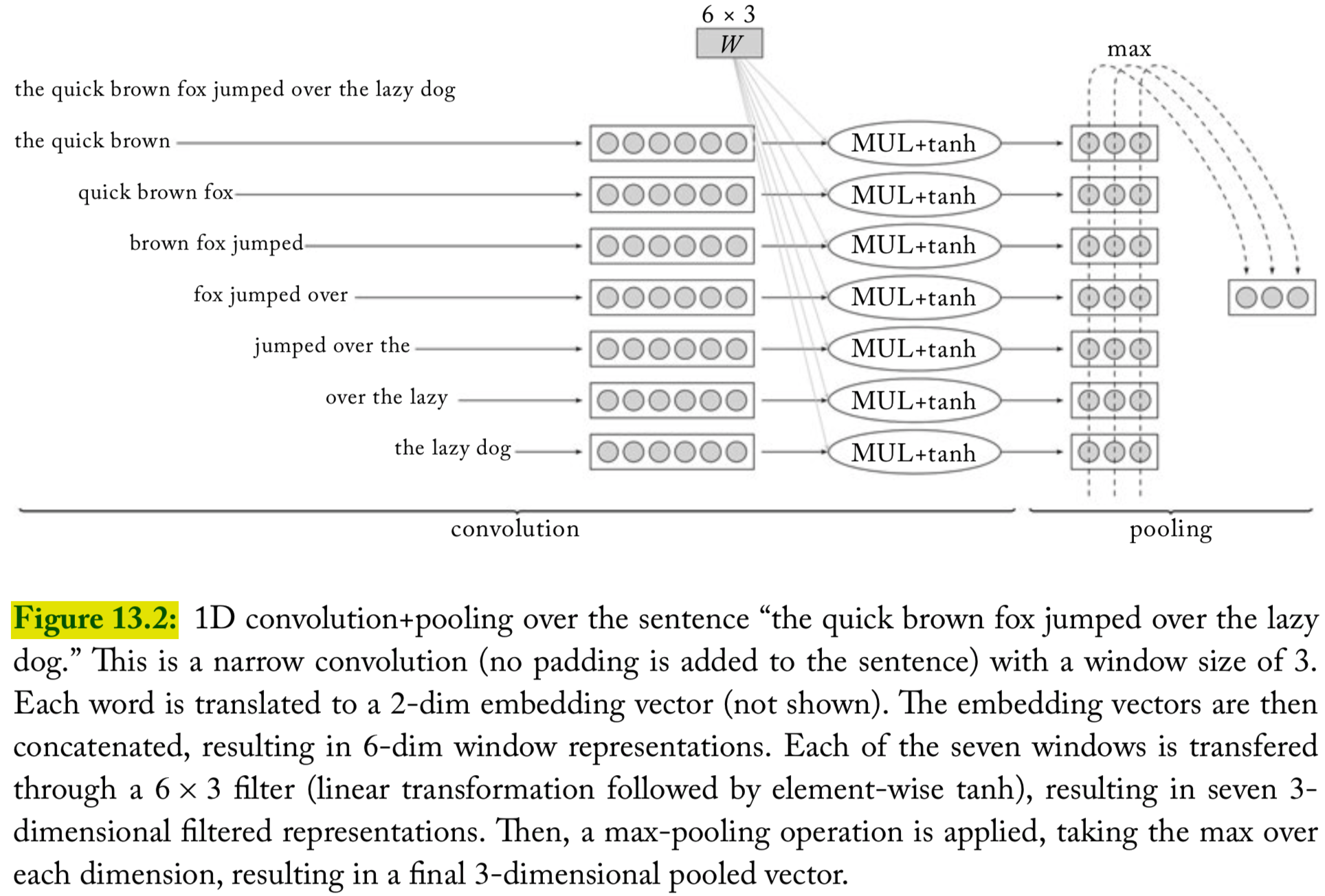
Convolution

• The main idea behind a convolution and pooling architecture of language tasks is to apply a non-linear (learned) function over each instantiation of a $k$-word sliding window over the sentence

• This function (also called “filter”) transforms a window of $k$ words into a scalar value

  • Intuitively, when the sliding window of size $k$ is run over a sequence, the filter function learns to identify informative $k$grams

• Several such filters can be applied, resulting in $\ell$ dimensional vector (each dimension corresponding to one filter) that captures important properties of the words in the window

Pooling

• Then a “pooling” operation is used to combine the vectors resulting from the different windows into a single $\ell$-dimensional vector, by taking the max or the average value observed in each of the $\ell$ dimensions over the different windows

  • The intention is to focus on the most important “features” in the sentence, regardless of their location

• The resulting $\ell$-dimensional vector is then fed further into a network that is used for prediction

1D convolutions over text

• A filter is a dot-product with a weight vector parameter $u$, which is often followed by nonlinear activation function

• Define the operation $\oplus \left(w_{i:i+k-1}\right)$ to be the concatenation of the vectors $w_i,\dots ,w_{i+k-1}$. The concatenated vector of the $i$th window is then $$x_i=\oplus \left(w_{i:i+k-1}\right)=[w_i;w_{i+1};\dots ;w_{i+k-1}]\in R^{k\cdot d_{\text{emb}}}$$

• Apply the filter to each window-vector, resulting scalar value $p_i$: $$\begin{array}{cc}& p_i=g(x_i\cdot u)\\ & p_i\in R,x_i\in R^{k\cdot d_{\text{emb}}},u\in R^{k\cdot d_{\text{emb}}}\end{array}$$

Joint formulation of 1D convolutions

• It is customary to use $\ell$ different filters $u_1,\dots ,u_{\ell }$, which can be arranged into a matrix $U$, and a bias vector $b$ is often added

$$\begin{array}{cc}& p_i=g(x_i\cdot U+b)\\ & p_i\in R^{\ell },x_i\in R^{k\cdot d_{\text{emb}}},U\in R^{k\cdot d_{\text{emb}}\times \ell },b\in R^{\ell }\end{array}$$

• Ideally, each dimension captures a different kind of indicative information

• The main idea behind the convolution layer: to apply the same parameterized function over all $k$grams in the sequence. This creates a sequence of $m$ vectors, each representing a particular $k$gram in the sequence

Narrow vs wide convolutions

• For a sentence of length $n$ with a window of size $k$

• Narrow convolutions: there are $n-k+1$ positions to start the sequence, and we get $n-k+1$ vectors $p_{1:n-k+1}$

• Wide convolutions: an alternative is to pad the sentence with $k-1$ padding-words to each side, resulting in $n+k+1$ vectors $p_{1:n+k+1}$

• We use $m$ to denote the number of resulting vectors

Vector pooling

• Applying the convolution over the text results in $m$ vectors $p_{1:m}$, each $p_i\in R^{\ell }$

• These vectors are then combined (pooled) into a single vector $c\in R^{\ell }$ representing the entire sequence

• During training, the vector $c$ is fed into downstream network layers (e.g., an MLP), culminating in an output layer which is used for prediction

Different pooling methods

• Max pooling: the most common, taking the maximum value across each dimension $j=1,\dots ,\ell$ $$c_{\left[j\right]}=\underset{1\le i\le m}{max}{p}_{i,\left[j\right]}$$

  • The effect of the max-pooling operation is to get the most salient information across window positions

• Average pooling $$c=\frac{1}{m}\sum _{i=1}^m{p}_i$$

• $K$-max pooling: the top $k$ values in each dimension are retained instead of only the best one, while preserving the order in which they appeared in the text

An illustration of convolution and pooling

Variations

• Rather than a single convolutional layer, several convolutional layers may be applied in parallel

• For example, we may have four different convolutional layers, each with a different window size in the range 2-5, capturing $k$gram sequences of varying lengths

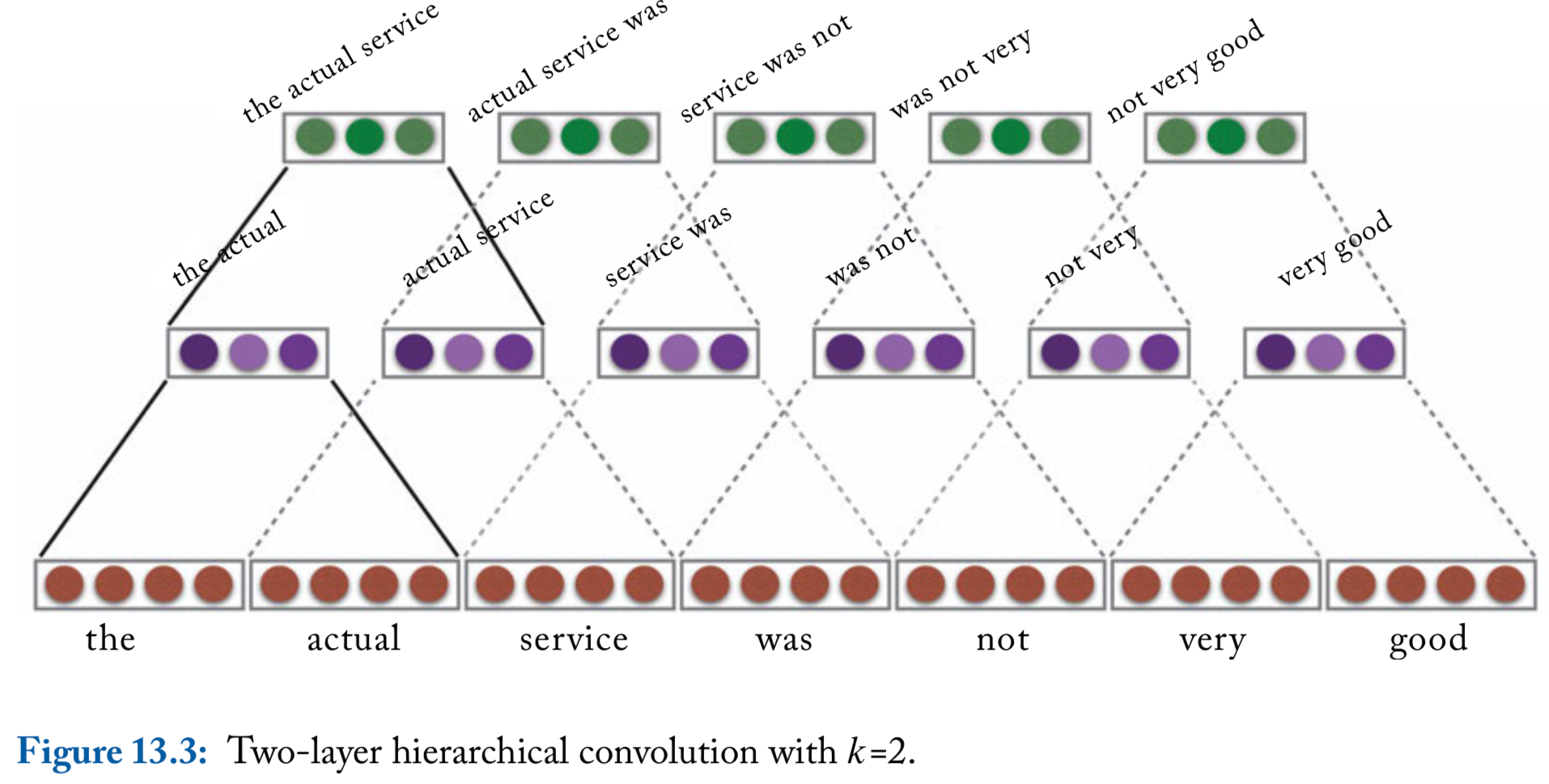
Hierarchical convolutions

• The 1D convolution approach described so far can the thought of as a ngram detector: a convolution layer with a window of size $k$ is learning to identify indicative $k$-gram in the input

$$p_{1:m}={\text{CONV}}_{U,b}^k\left(w_{1:n}\right)$$

• We can extend this into a hierarchy of convolutional layers with $r$ layers that feed into each other $$\begin{array}{cc}{p}_{1:m_1}^1& ={\text{CONV}}_{U^1,b^1}^{k_1}\left(w_{1:n}\right)\\ p_{1:m_2}^2& ={\text{CONV}}_{U^2,b^2}^{k_2}\left(p_{1:m_1}^1\right)\\ & \cdots \\ p_{1:m_r}^r& ={\text{CONV}}_{U^r,b^r}^{k_r}\left(p_{1:m_{r-1}}^{r-1}\right)\end{array}$$

Hierarchical convolutions, continued

• For $r$ layers with a window of size $k$, each vector $p_i^r$ will be sensitive to a window of $r(k-1)+1$ words

• Moreover, the vector $p_i^r$ can be sensitive to gappy-ngrams of $k+r-1$ works, potentially capturing patterns such as “not ___ good” or “obvious ___ predictable ___ plot”, where ___ stands for a short sequence of words

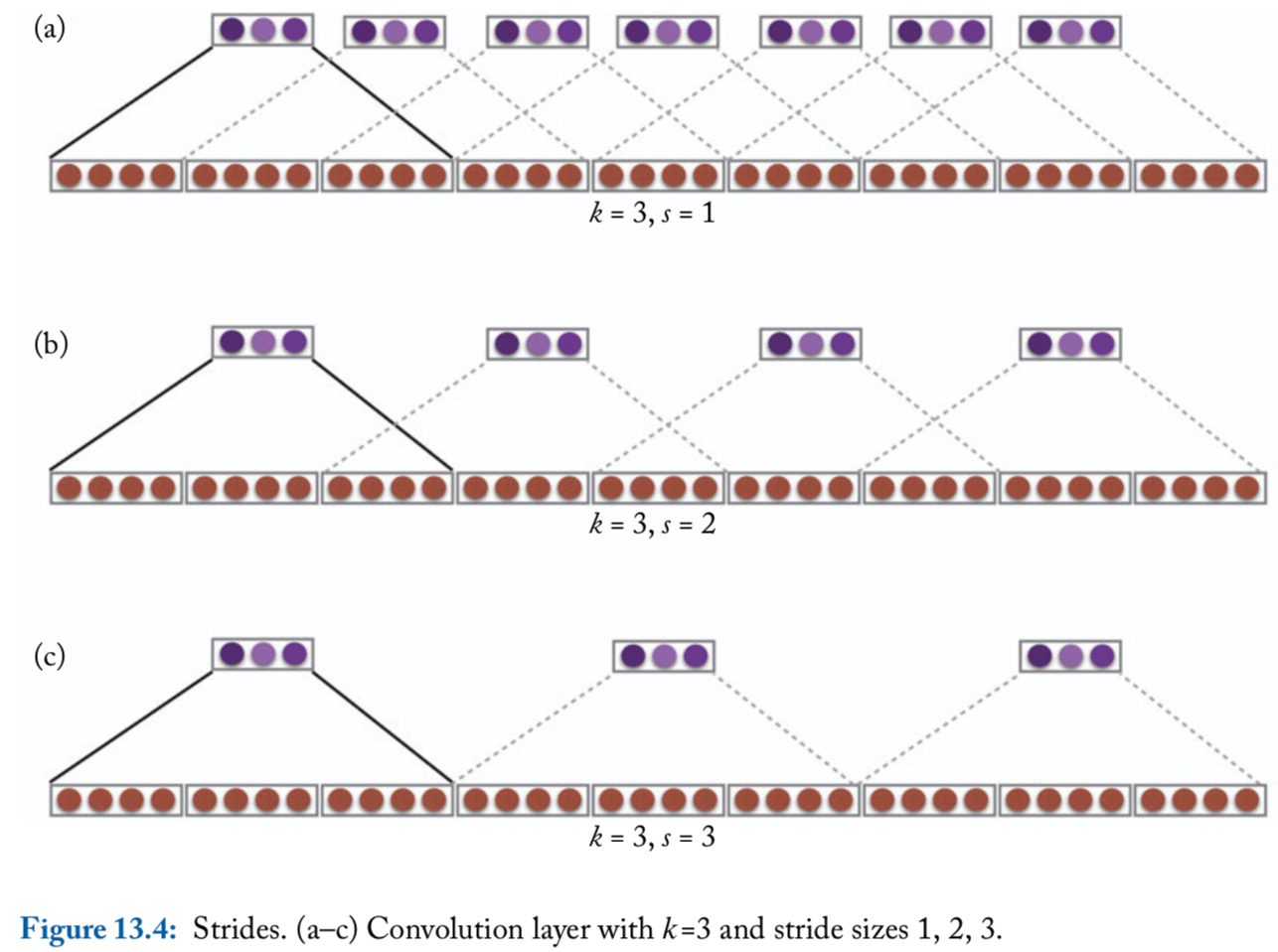
Strides

• So far, the convolution operation is applied to each $k$-word window in the sequence, i.e., windows starting at indices $1,2,3,\dots$. This is said to have a stride of size $1$

• Larger strides are also possible. For example, with a stride of size $2$, the convolution operation will be applied to windows starting at indices $1,3,5,\dots$

• Convolution with window size $k$ and stride size $s$: $$\begin{array}{cc}{p}_{1:m}& ={\text{CONV}}_{U,b}^{k,s}\left(w_{1:n}\right)\\ p_i& =g(\oplus \left(w_{1+(i-1)s:(s+k)i}\right)\cdot U+b)\end{array}$$

An illustration of stride size

References

• Goldberg, Yoav. (2017). Neural Network Methods for Natural Language Processing, Morgan & Claypool