For the pdf slides, click here
Ch14 Recurrent Neural Networks: Modeling Sequences and Stacks
RNNs overview
RNNs allow representing arbitrarily sized sequential inputs in fixed-sized vectors, while paying attention to the structured properties of the inputs
This chapter describes RNNs as an abstraction: an interface for translating a sequence of inputs into a fixed sized output, that can be plugged as components in larger networks
RNNs allow for language models that do not make the markov assumption, and condition the next word on the entire sentence history
It is important to understand that the RNN does not do much on its own, but serves as a trainable component in a larger network
The RNN Abstraction
The RNN abstraction
On a high level, the RNN is a function that
- Takes as input an arbitrary length ordered sequence of -dimensional vectors , and
- Returns as output a single dimensional vector
- The output vector is then used for further prediction
This implicitly defines an output vector for each prefix . We denote by RNN the function returning this sequence
The RNN function provides a framework for conditioning on the entire history without the Markov assumption
The R function and the O function
The RNN is defined recursively, by means of a function taking as the state vector and an input vector and returning a new state vector
The state vector is then mapped to an output vector using a simple deterministic function
The functions and are the same across the sequence positions, but the RNN keeps track of the states of computation through the state vector that is kept and being passed across invocations of
An illustration of the RNN
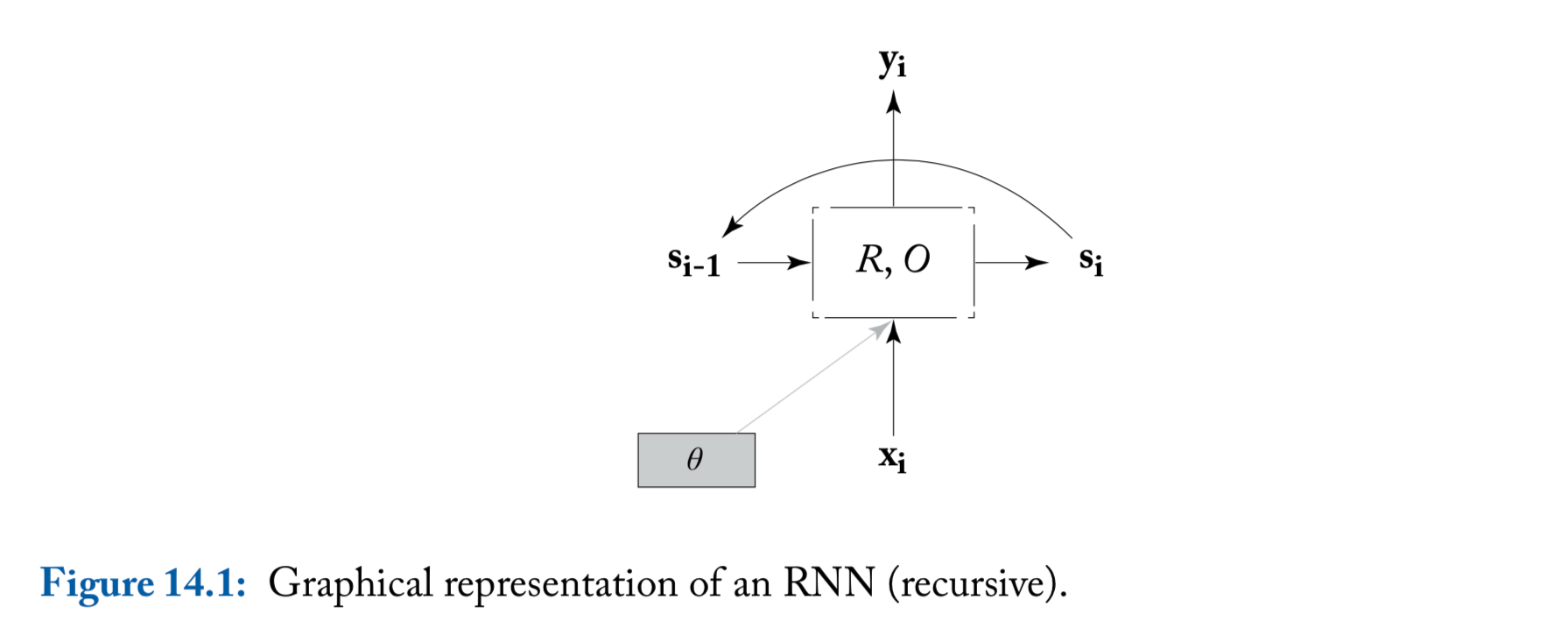
- We include here the parameters in order to highlight the fact that the same parameters are shared across all time steps
An illustration of the RNN (unrolled)
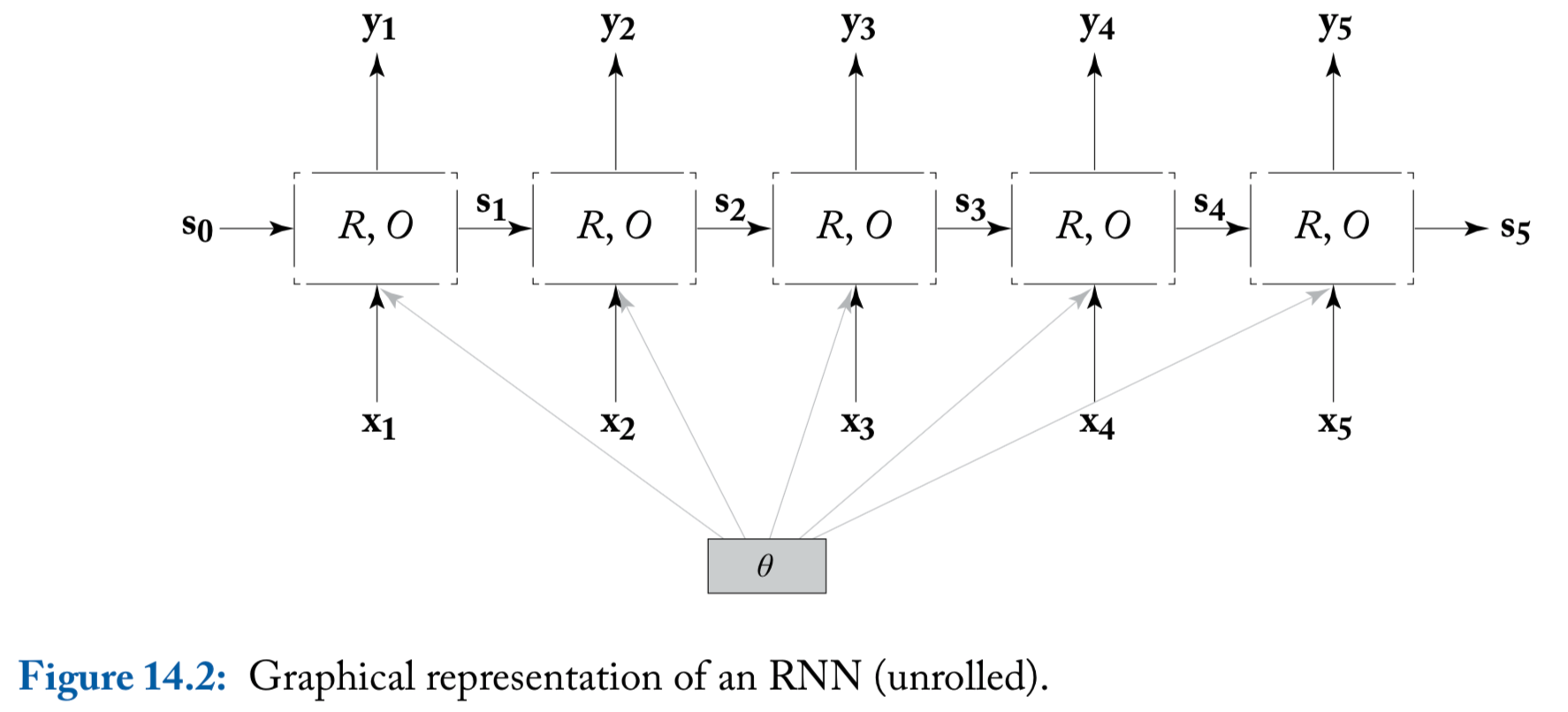
Common RNN usages
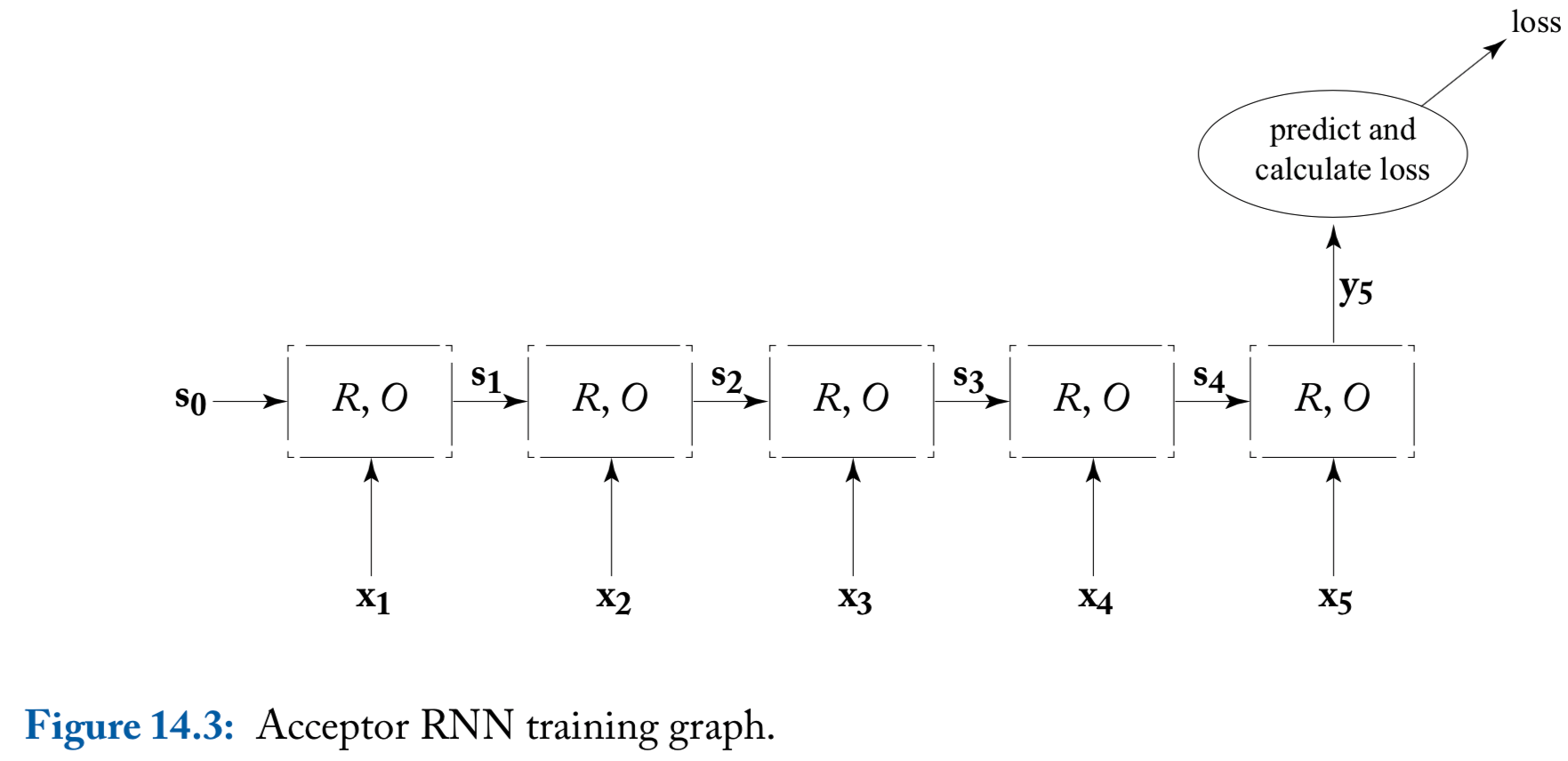
Common RNN usage patterns: acceptor
Acceptor: based on the supervision signal only at the final output vector
- Typically, the RNN’s output vector is fed into a fully connected layer or an MLP, which produce a prediction
Common RNN usage patterns: encoder
- Encoder: also only uses the final output vector . Here is treated as an encoding of the information in the sequence, and is used as additional information together with other signals
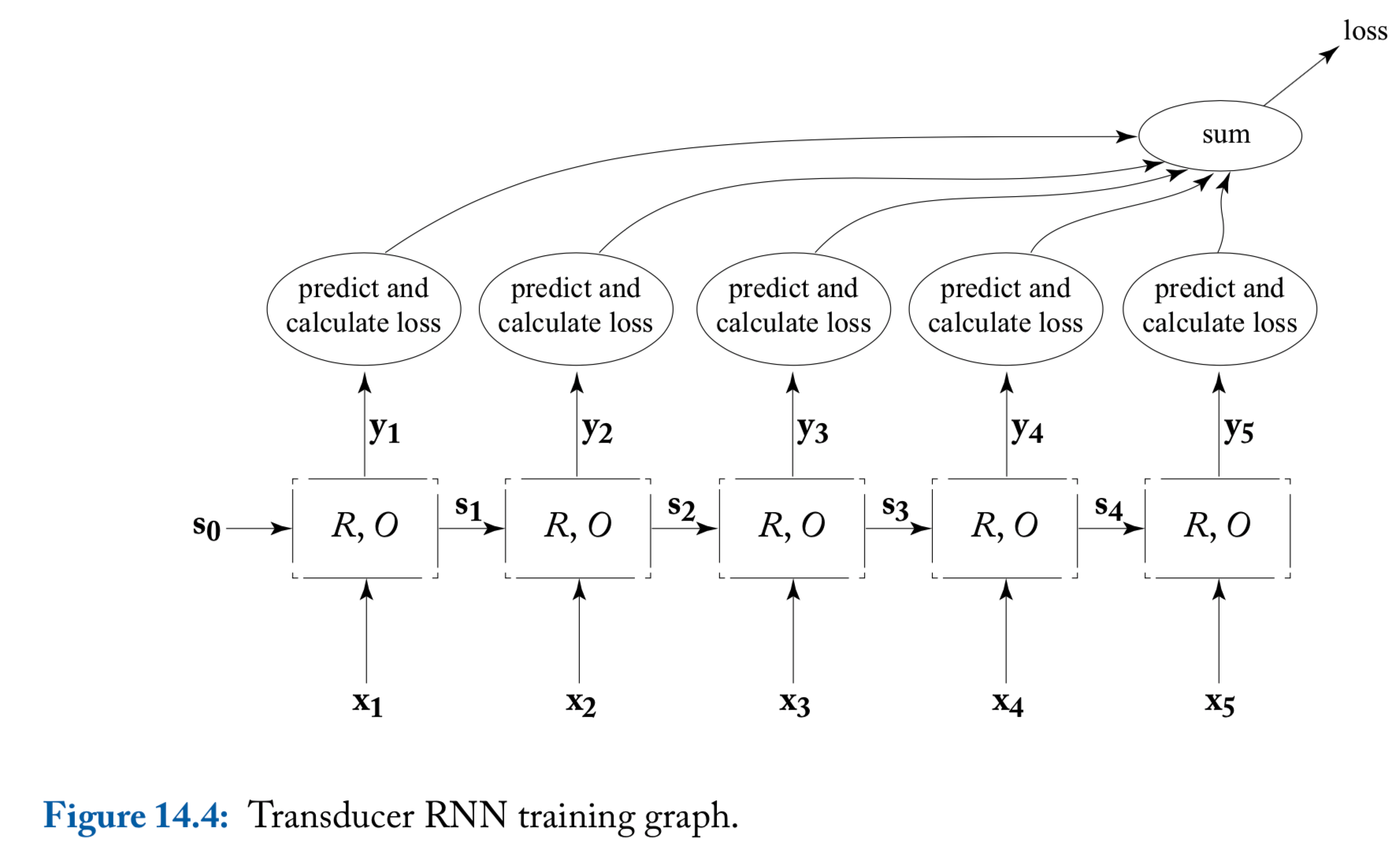
Common RNN usage patterns: transducer
Transducer: The loss of unrolled sequence will be used
A natural use case of the transduction is for language modeling, where the sequence of words is used to predict a distribution over the th word
RNN based lanuage models are shown to provide vastly better perplxities than traditional language models
Using RNNs as transducers allows us to relax the Markov assumption and condition on the entire prediction history
An illustration of transducer
Bidirectional RNNs and Deep RNNs
Bidirectional RNNs (biRNN)
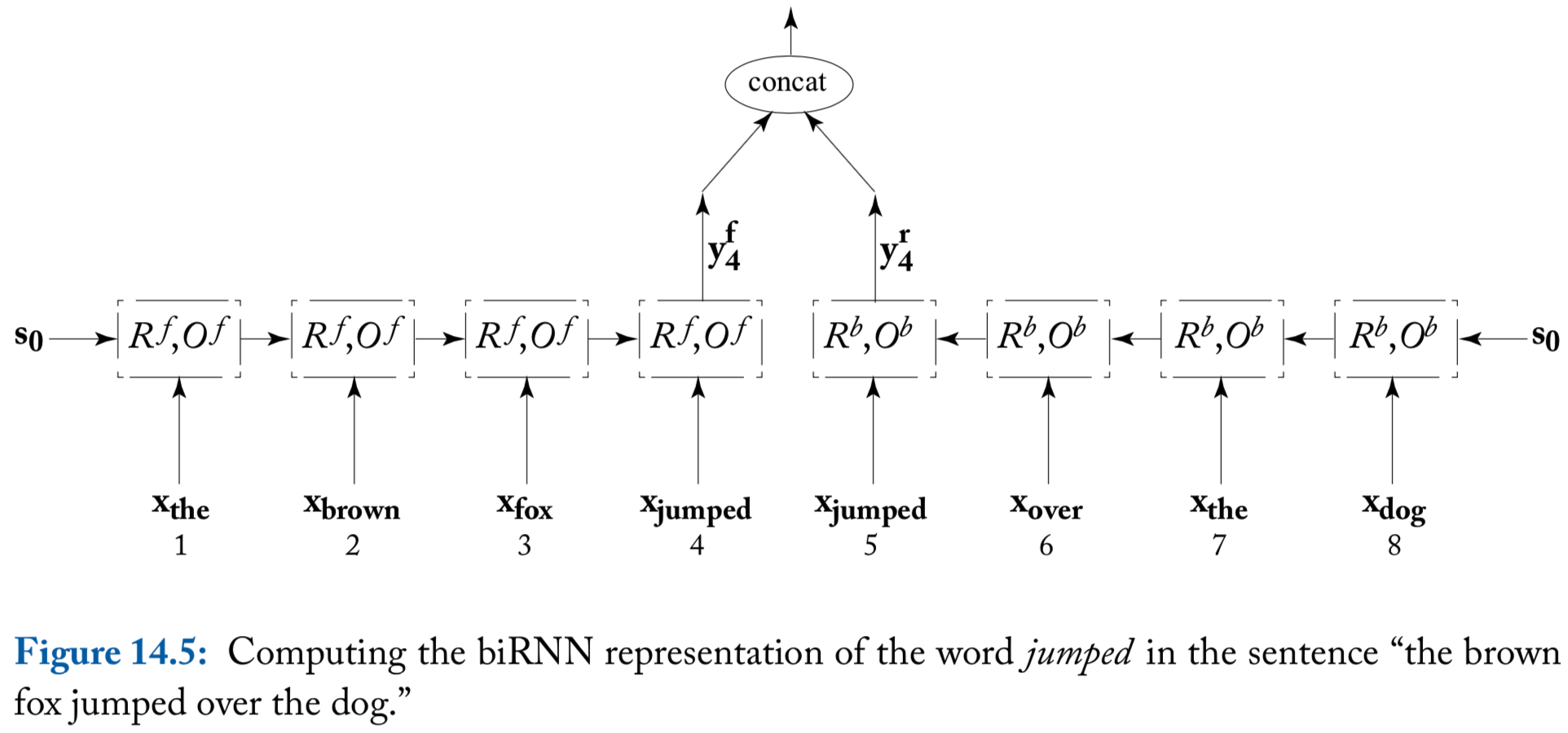
A useful elaboration of an RNN is a biRNN
Consider an input sequence . The biRNN works by maintaining two separate states, and for each input position
- The forward state is based on
- The backward state is based on
The output at position is based on the concatenation of the two output vectors
Thus, we define biRNN as
An illustration of biRNN
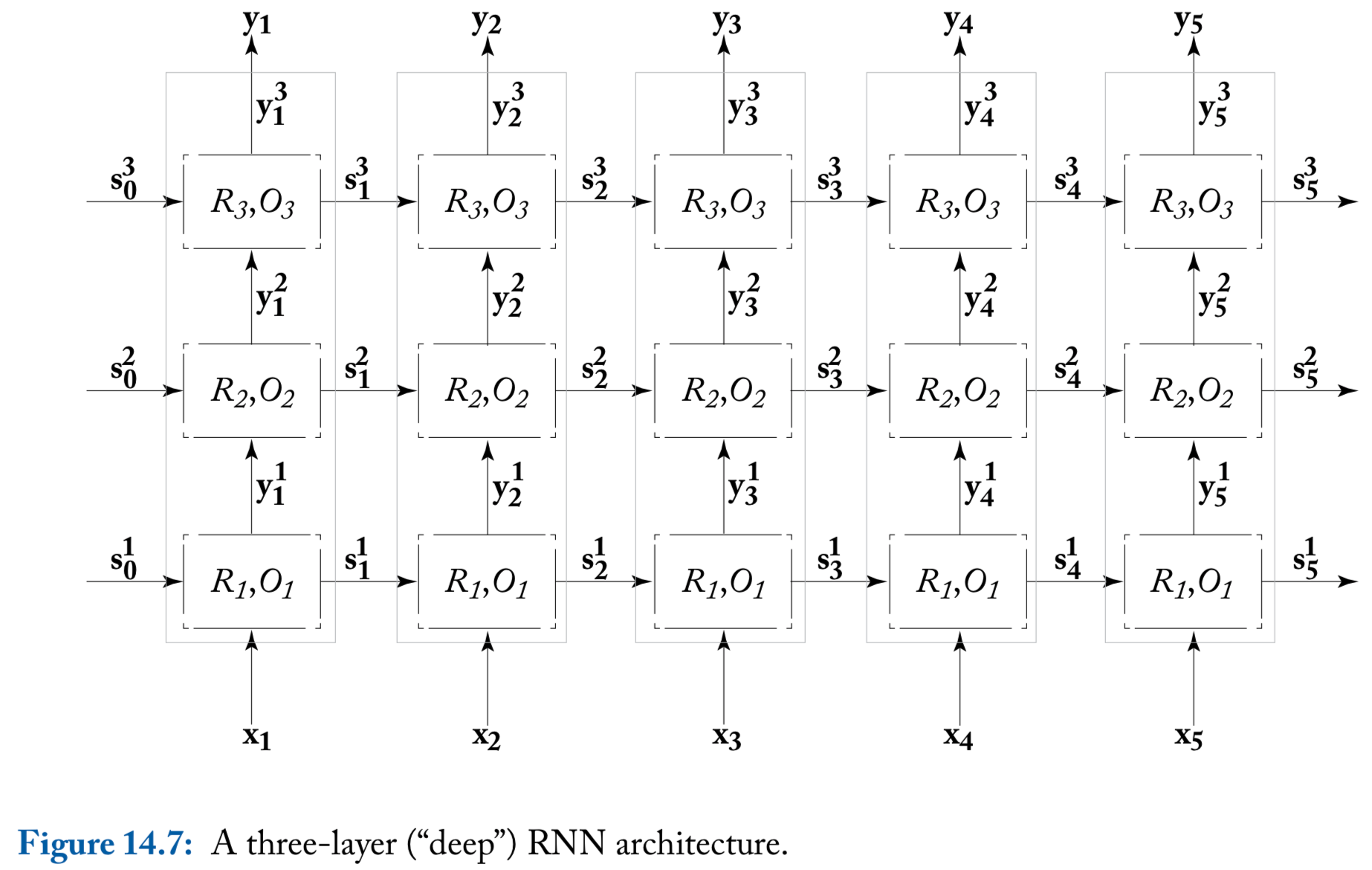
Deep (multi-layer stacked) RNNs
The input for the first RNN are , while the input of the th RNN () are the outputs of the RNN below it,
While it is not theoretically clear what is the additional power gained by the deeper architecture, it was observed empirically that deep RNNs work better than shallower ones on some tasks
The author’s experience: using two or more layers indeed often improves over using a single one
A note on reading the literature
Unfortunately, it is often the case that inferring the exact model form from reading its description in a research paper can be quite challenging
- For example,
- The inputs to the RNN can be either one-hot vectors or embedded representations
- The input sequence can be padded with start-of-sequence and/or end-of-sequence symbols, or not
An illustration of deep RNN
Ch15 Concrete Recurrent Neural Network Architectures
Simple RNN
Simple RNN (SRNN)
- The nonlinear function is usually tanh or ReLU
The output function is the identify function
SRNN is hard to train effectively because of the vanishing gradients problem
Gated Architectures: LSTM and GRU
Gated architectures
An apparent problem with SRNN is that the memory access is not controlled. At each step of the computation, the entire memory state is read, and the entire memory state is written
We denote the hadamard-product operation (element-wise product) as
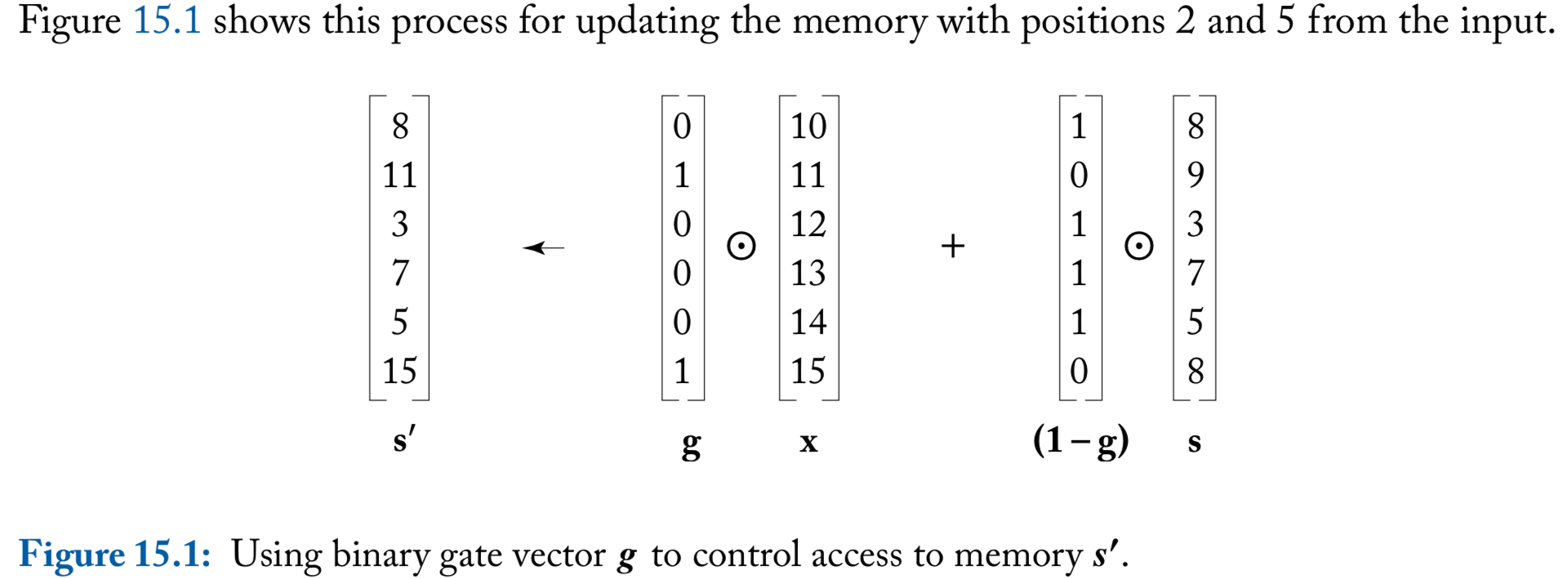
To control memory access, consider a binary vector
For a memory and an input , the computation
“reads” the entries in that correspond to the 1 values in , and writes them to the new memory . Locations that weren’t read to are copied from the memory to the new memory through the use of the gate
An illustration of binary gate
Differentiable gates
The gates should not be static, but be controlled by the current memory state and the input, and their behavior should be learned
Obstacle: learning in our framework entails being differentiable (because of the backpropagation algorithm), but the binary 0-1 values used in th e gates are not differentiable
Solution: approximate the hard gating mechanism with a soft, but diffrentiable, gating mechanism
To achieve these differentiable gates, we replace the requirement that , and allow arbitrary real numbers . These are then passed through a sigmoid function , which take values in the range
LSTM
- Long Short-Term Memory (LSTM): explicitly splits the state vector into two halves, where one half is treated as “memory cells” , and the hidden state component
- There are three gates, nput, orget, and utput
LSTM gates
The gates are based on and are passed through a sigmoid activation function
When training LSTM networks, it is strongly recommended to always initialize the bias term of the forget gate to be close to one
GRU
Gated Recurrent Unit (GRU) is shown to perform comparably to the LSTM on several datasets
GRU has substantially fewer gates that LSTM and doesn’t have a separate memory component
- Gate controls access to the previous state in
Gate controls the proportions of the interpolation between and when in the updated state
Ch16 Modeling with Recurrent Networks
Sentiment Classification
Acceptors
The simplest use of RNN: read in an input sequence, and produce a binary of multi-class answer at the end
The power of RNN is often not needed for many natural language classification tasks, because the word-order and sentence structure turn out to not be very important in many cases, and bag-of-words or bag-of-ngrams classifier often works just as well or even better than RNN acceptors
Sentiment classification: sentence level
The sentence level sentiment classification is straightforward to model using an RNN acceptor:
- Tokenization
- RNN reads in the words of the sentence one at a time
- The final RNN state is then fed into a MLP followed by a softmax-layer with two outputs
- The network is trained with cross-entropy loss based on the gold sentiment labels
biRNN: it is often helpful to extend the RNN model into the biRNN
Hierarchical biRNN
For longer sentences, it can be useful to use a hierarchical architecture, in which the sentence is split into smaller spans based on punctuation
Suppose a sentence is split into spans , then the architecture is
Each of the different spans may convey a different sentiment
The higher-level acceptor reads the summary produced by the lower level encoder, and decides on the overall sentiment
Document level sentiment classification
Document level sentiment classification and harder than sentence level classification
A hierarchical architecture is useful:
- Each sentence is encoded using a gated RNN, producing a vector
- The vectors are then fed into a second gated RNN, producing a vector
- is then used fro prediction
Keeping all intermediate vectors of the document-level RNN produces slightly higher results in some cases
References
- Goldberg, Yoav. (2017). Neural Network Methods for Natural Language Processing, Morgan & Claypool