For the pdf slides, click here
Confounding
Confounding
Confounders: variables that affect both the treatment and the outcome
If we assign treatment based on a coin flip, since the coin flip doesn’t affect the outcome, it’s not a confounder
If older people are at higher risk of heart disease (the outcome) and are more likely to receive the treatment, then age is a confounder
To control for confounders, we need to
- Identify a set of variables that will make the ignorability assumption hold
- Causal graphs will help answer this question
- Use statistical methods to control for these variables and estimate causal effects
Causal Graphs
Overview of graphical models
Encode assumption about relationship among variables
- Tells use which variables are independent, dependent, conditionally independent, etc
Terminologies of Directed Acyclic Graphs (DAGs)
Terminology of graphs
- Directed graph: shows that affects
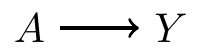
- Undirected graph: and are associated with each other
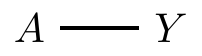
Nodes or vertices: and
- We can think of them as variables
Edge: the link between and
Directed graph: all edges are directed
Adjacent variables: if connected by an edge
Paths
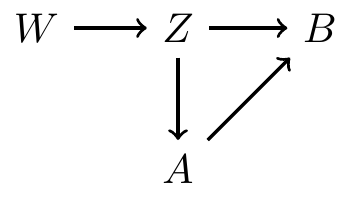
A path is a way to get from one vertex to another, traveling along edges
- There are 2 paths from to :
Directed Acyclic Graphs (DAGs)
- No undirected paths
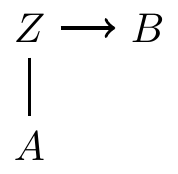
- No cycles
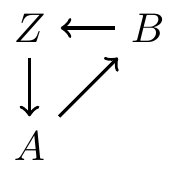
- This is a DAG
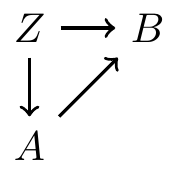
More terminology
- is ’s parent
- has two parents, and
- is a child of
- is a descendant of
- is a ancestor of
Relationship between DAGs and probability distributions
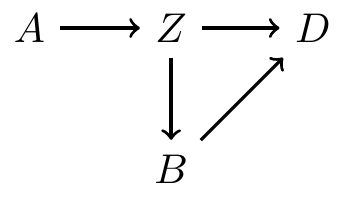
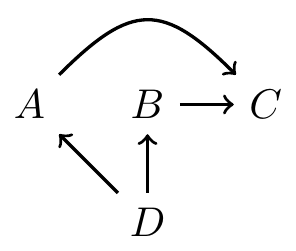
DAG example 1
C is independent of all variables
and are independent, conditional on
and are marginally dependent
DAG example 2
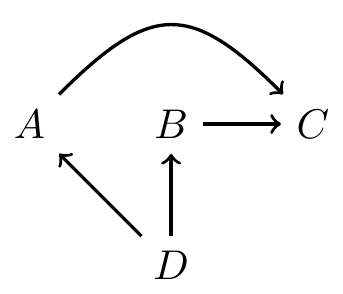
and are independent, conditional on and
and are independent, conditional on and
Decomposition of joint distributions
Start with roots (nodes with no parents)
Proceed down the descendant line, always conditioning on parents
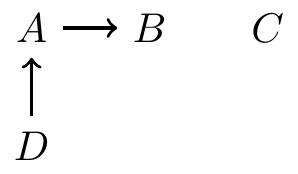
Compatibility between DAGs and distributions
In the above examples, the DAGs admit the probability factorizations. Hence, the probability function and the DAG are compatible
DAGs that are compatible with a particular probability function are not necessarily unique
Example 1:
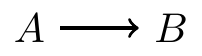
- Example 2:
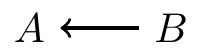
- In both of the above examples, and are dependent, i.e.,
Types of paths, blocking, and colliders
Types of paths
- Forks
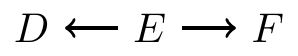
- Chains
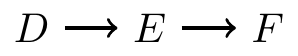
- Inverted forks
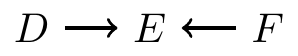
When do paths induce associations?
If nodes and are on the ends of a path, then they are associated (via this path), if
- Some information flows to both of them (aka Fork), or
- Information from one makes it to the other (aka Chain)
Example: information flows from to and
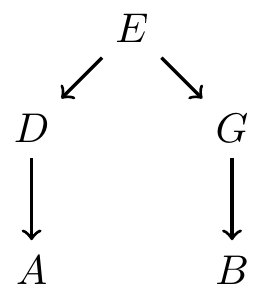
- Example: information from makes it to
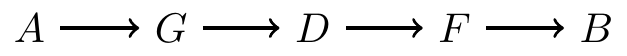
Paths that do not induce association
- Information from and collide at
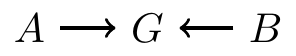
is a collider
and both affect :
- Information does not flow from to either or
- So and are independent (if this is the only path between them)
If there is a collider anywhere on the path from to , then no association between and comes from this path
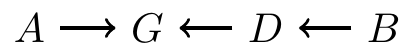
Blocking on a chain
Paths can be blocked by conditioning on nodes in the path
In the graph below, is a node in the middle of a chain. If we condition on , then we block the path from to
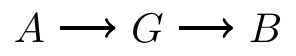
- For example, is the temperature, is whether sidewalks are icy, and is whether someone falls
- and are associated marginally
- But if we conditional on the sidewalk condition , then and are independent
Blocking on a fork
Associations on a fork can also be blocked
In the following fork, if we condition on , then the path from to is block
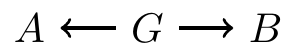
No need to to block a collider
- The opposite situation occurs if a conllider is blocked
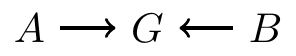
In the following inverted fork
- Originally and are not associated, since information collides at
- But if we condition on , then and become associated
Example: and are the states of two on/off switches, and is whether the lightbulb is lit up.
The two switches and are determined by two independent coin flips
is lit up only if both and are in the on state
Conditional on , the two switches are not independent: if is off, then must be off if is on
d-separation
d-separation
A path is d-separated by a set of nodes if
It contains a chain () and the middle part is in , or
It contains a fork () and the middle part is in , or
It contains an inverted fork (), and the middle part is not in , nor are any descendants of it
Two nodes, and , are d-separated by a set of nodes if it blocks every path from to . Thus
Recall the ignorability assumption
Confounders on paths
- A simple DAG: is a confounder between the relationship between treatment and outcome
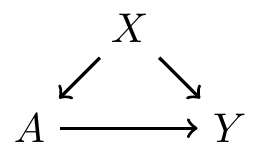
A slightly more complicated graph
- affects directly
- affects indirectly, through
- Thus, is a confounder
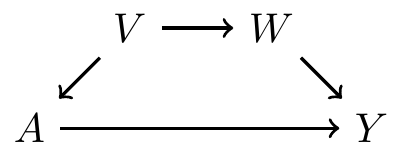
Frontdoor and backdoor paths
Frontdoor paths
A frontdoor path from to is one that begins with an arrow emanating out of
We do not worry about frontdoor paths, because they capture effects of treatment
Example: is a frontdoor path from to
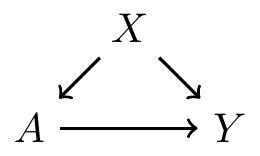
- Example: is a frontdoor path from to
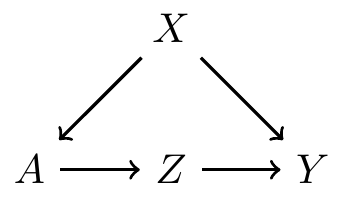
Do not block nodes on the frontdoor path
If we are interested in the causal effect of on , we should not control for (aka block)
- This is because controlling for would be controlling for an affect of treatment
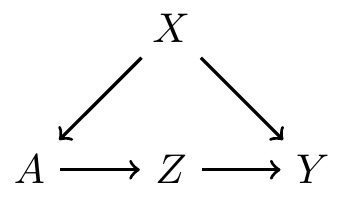
- Causal mediation analysis involves understanding frontdoor paths from and
Backdoor paths
Backdoor paths from treatment to outcome are paths from to that travels through arrows going into
Here, is a backdoor path from to
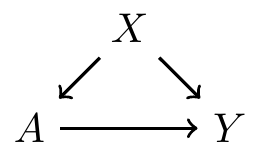
Backdoor paths confound the relationship between and , so they need to be blocked!
To sufficiently control for confounding, we must identify a set of variables that block all backdoor paths from treatment to outcome
- Recall the ignorability: if is this set of variables, then
Criteria
Next we will discuss two criteria to identify sets of variables that are sufficient to control for confounding
- Backdoor path criterion: if the graph is known
- Disjunctive cause criterion: if the graph is not known
Backdoor path criterion
Backdoor path criterion
Backdoor path criterion: a set of variables is sufficient to control for confounding if
- It blocks all backdoor paths from treatment to the outcome, and
- It does not include any descendants of treatment
Note: the solution is not necessarily unique
Backdoor path criterion: a simple example
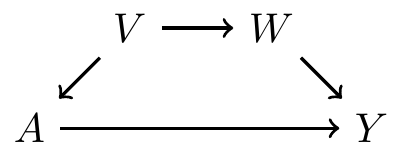
There is one backdoor path from to
- It is not blocked by a collider
Sets of variables that are sufficient to control for confounding:
- , or
- , or
Backdoor path criterion: a collider example
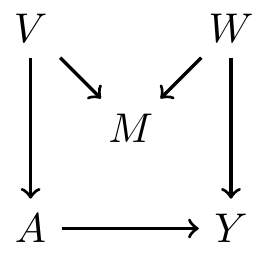
There is one backdoor path from to
- It is blocked by a collider , so there is no confounding
If we condition on , then it open a path between and
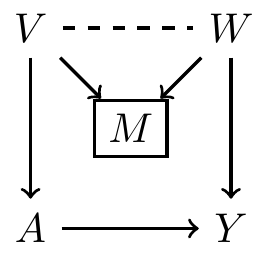
- Sets of variables that are sufficient to control for confounding:
- , , , , ,
- But not
Backdoor path criterion: a multi backdoor paths example
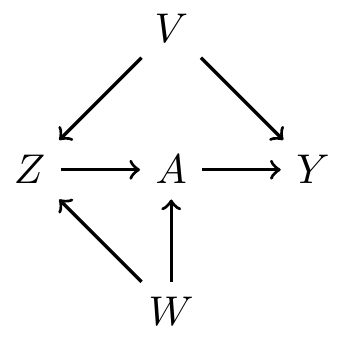
First path:
- No collider on this path
- So controlling for either , , or both is sufficient
Second path:
- is a collider
- So controlling opens a path between and
- We can block , , , , or
To block both paths, it’s sufficient to control for
- , , , or
- But not or
Disjunctive cause criterion
Disjunctive cause criterion
- For many problems, it is difficult to write down accurate DAGs
In this case, we can use the disjunctive cause criterion: control for all observed causes of the treatment, the outcome, or both
If there exists a set of observed variables that satisfy the backdoor path criterion, then the variables selected based on the disjunctive cause criterion are sufficient to control for confounding
Disjunctive cause criterion does not always select the smallest set of variable to control for, but it is conceptually simple
Example
Observed pre-treatment variables:
Unobserved pre-treatment variables:
Suppose we know: are causes of , or both
Suppose is not a cause of either or
- Comparing two methods for selecting variables
- Use all pre-treatment covariates:
- Use variables based on disjunctive cause criterion:
Example continued: hypothetical DAG 1
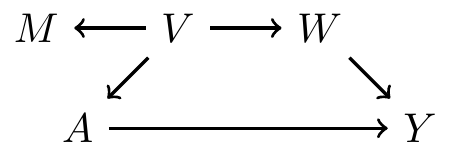
- Use all pre-treatment covariates:
- Satisfy backdoor path criterion? Yes
- Use variables based on disjunctive cause criterion:
- Satisfy backdoor path criterion? Yes
Example continued: hypothetical DAG 2
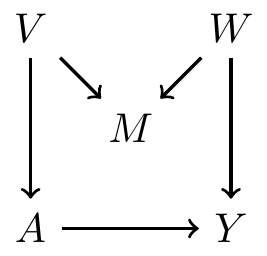
- Use all pre-treatment covariates:
- Satisfy backdoor path criterion? Yes
- Use variables based on disjunctive cause criterion:
- Satisfy backdoor path criterion? Yes
Example continued: hypothetical DAG 3
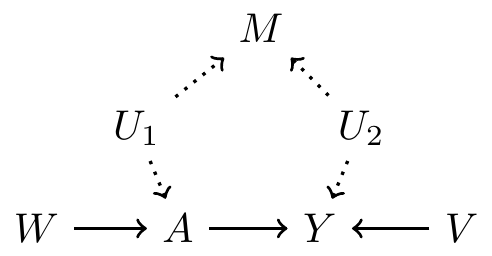
- Use all pre-treatment covariates:
- Satisfy backdoor path criterion? No
- Use variables based on disjunctive cause criterion:
- Satisfy backdoor path criterion? Yes
Example continued: hypothetical DAG 4
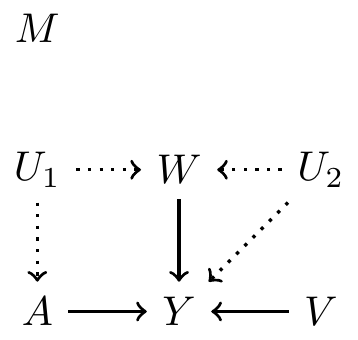
- Use all pre-treatment covariates:
- Satisfy backdoor path criterion? No
- Use variables based on disjunctive cause criterion:
- Satisfy backdoor path criterion? No
References
Coursera class: “A Crash Course on Causality: Inferring Causal Effects from Observational Data”, by Jason A. Roy (University of Pennsylvania)