Course Notes: A Crash Course on Causality -- Week 4: Inverse Probability of Treatment Weighting (IPTW)

For the pdf slides, click here

Inverse Probability of Treatment Weighting

Motivating example

  • Suppose there is a single confounder \(X\), with propensity scores \[ P(A=1\mid X=1) = 0.1, \quad P(A=1\mid X=0) = 0.8 \]

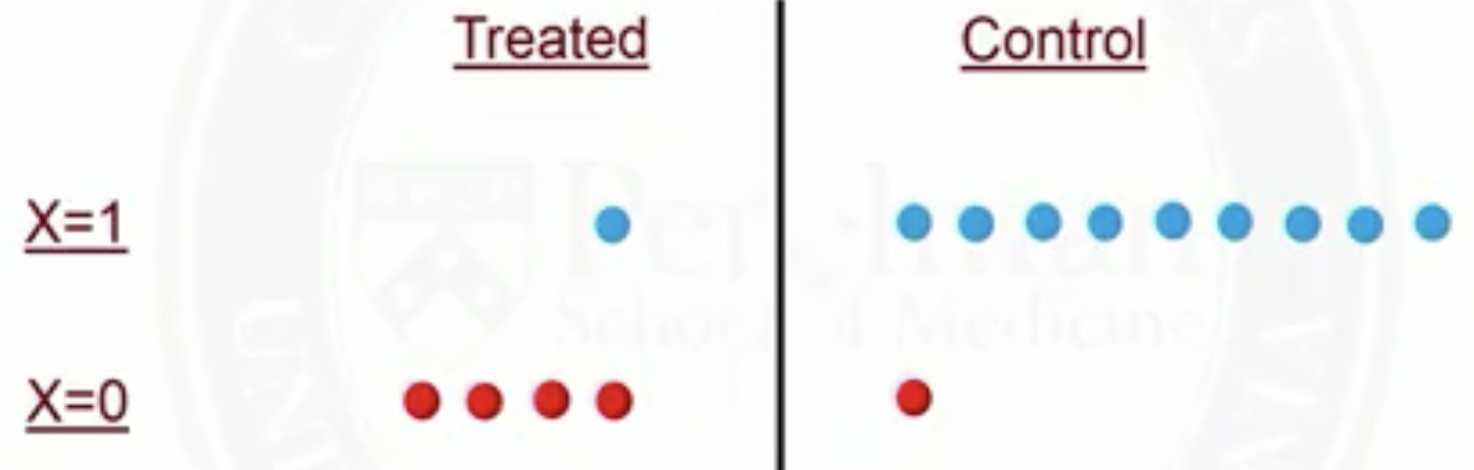
  • In propensity score matching, for subjects with \(X=1\), 1 out of 9 controls will be matched to the treated

    • Thus, 1 person in the treated group counts the same as 9 people from the control group

    • So rather than matching, we could use all data, but down-weight each control subject to be just 1/9 of the treated subject

Inverse probability of treatment weighting (IPTW)

  • IPTW weights: inverse of the probability of treatment received

    • For treated subjects, weight by \(1/P(A=1\mid X)\)
    • For control subjects, weight by \(1/P(A=0\mid X)\)

  • In the previous example

    • For \(X=1\), the weight for a treated subject is \(1/0.1 = 10\), and the weight for a control subject is \(1/0.9 = \frac{10}{9}\)

    • For \(X=0\), the weight for a treated subject is \(1/0.8 = \frac{5}{4}\), and the weight for a control subject is \(1/0.2 = 5\)

  • Motivation: in survey sampling, it is common to oversample some subpopulation, and then use Horvitz-Thompson estimator to estimate population means

Pseudo population

  • IPTW creates a pseudo-population where treatment assignment no longer depend on \(X\)

    • So there is no confounding in the pseudo-population

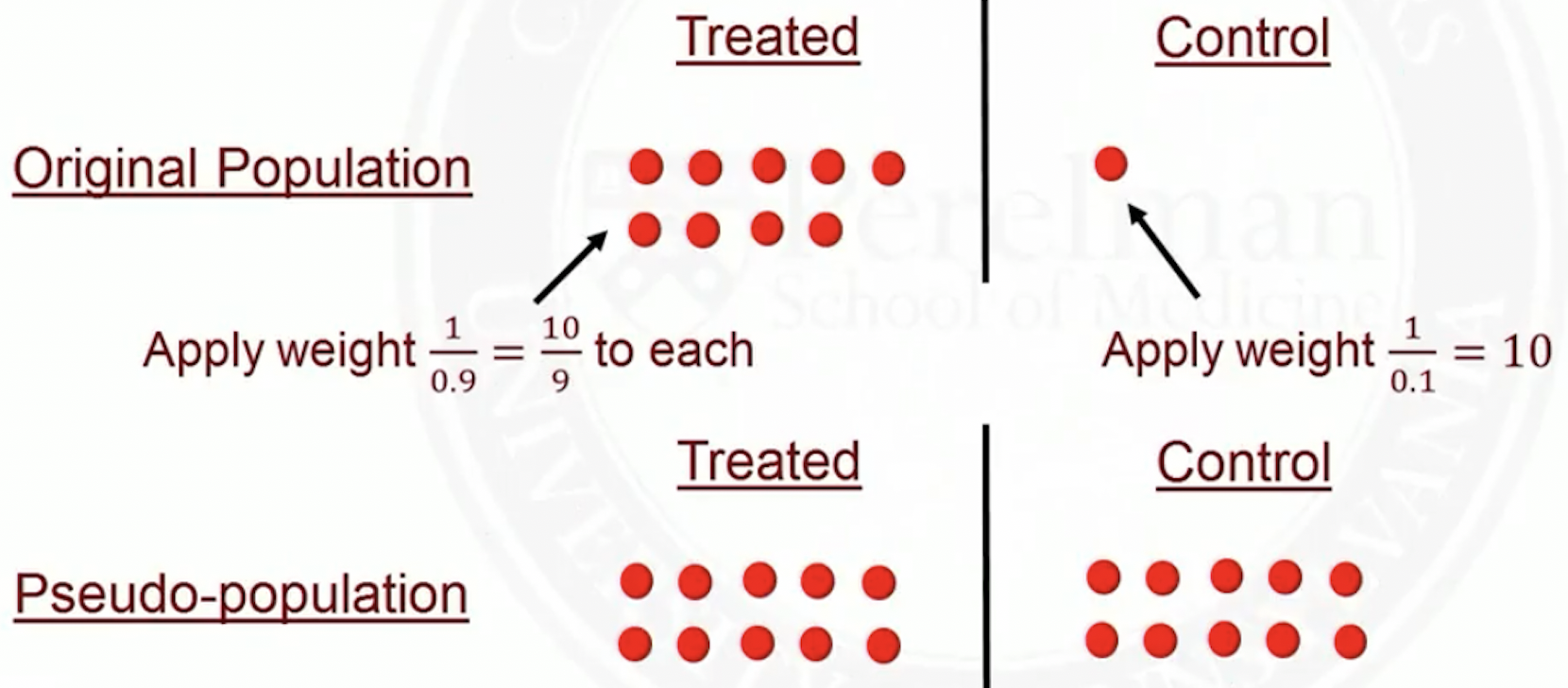
  • In the original population, some people were more likely to get treated based on their \(X\)’s

  • In the pseudo-population, everyone is equally likely to get treated, regardless of their \(X\)’s

Estimation with IPTW

  • We can estimate \(E(Y^1)\) as below \[ \frac{\sum_{i=1}^n \frac{1}{\pi_i} A_i Y_i} {\sum_{i=1}^n \frac{1}{\pi_i} A_i } \]

    • where \(\pi_i = P(A_i=1|X_i)\) is the propensity score
    • The numerator is the sum of \(Y\)’s in treated pseudo-population
    • The denominator is the number of subjects in treated pseudo-population

  • We can estimate \(E(Y^0)\) as below \[ \frac{\sum_{i=1}^n \frac{1}{1-\pi_i} (1-A_i) Y_i} {\sum_{i=1}^n \frac{1}{1-\pi_i} (1-A_i) } \]

  • Average treatment effect: \(E(Y^1) - E(Y^0)\)

Marginal Structural Models

Marginal structural models

  • Marginal structural models (MSM): a model for the mean of the potential outcomes

  • Marginal: not conditional on the confounders (population average)

  • Structural: for potential outcomes, not observed outcomes

Linear MSM and logistic MSM

  • Linear MSM \[ E(Y^a) = \psi_0 + \psi_1 a, \quad a = 0, 1 \]

    • \(E(Y^0) = \psi_0\), \(E(Y^0) = \psi_0 + \psi_1\)
    • So the average causal effect \[E(Y^1) - E(Y^0) = \psi_1\]

  • Logistic MSM \[ logit\{E(Y^a)\} = \psi_0 + \psi_1 a, \quad a = 0, 1 \]

    • So the causal odds ratio \[ \frac{\frac{P(Y^1=1)}{1-P(Y^1=1)}}{\frac{P(Y^0=1)}{1-P(Y^0=1)}} = \psi_1 \]

MSM with effect modification

  • Suppose \(V\) is a variable that modifies the effect of \(A\)

  • A linear MSM with effect modification \[ E(Y^a \mid V) = \psi_0 + \psi_1 a + \psi_3V + \psi_4 a V, \quad a = 0, 1 \]

    • So the average causal effect \[E(Y^1) - E(Y^0) = \psi_1 + \psi_4 V\]
  • General MSM \[ g\{E(Y^a \mid V)\} = h(a, V; \psi) \]
    • \(g()\): link function
    • \(h()\): a function specifying parametric from of \(a\) and \(V\) (typically additive, linear)

MSM estimation using pseudo-population

  • Because of confounding, MSM \[ g\{E(Y^a \mid V)\} = \psi_0 + \psi_1 a \] is difference from GLM (generalized linear model) \[ g\{E(Y_i \mid A_i)\} = \psi_0 + \psi_1 A_i \]

  • Pseudo-population (obtained from IPTW) is free of confounding

    • We therefore estimate MSM by solving GLM with IPTW

MSM estimation steps

  1. Estimate propensity score, using logistic regression

  2. Create weights

    • Inverse of propensity score for treated subjects
    • Inverse of one minus propensity score for control subjects

  3. Specify the MSM of interest

  4. Use software to fit a weighted generalized linear model

  5. Use asymptotic (sandwich) variance estimator

    • This accounts for fact that pseudo-population might be larger than sample size

Bootstrap

  • We may also use bootstrap to estimate standard error

  • Bootstrap steps

    1. Randomly sample with replacement from the original sample

    2. Estimate parameters

    3. Repeat steps 1 and 2 many times

    4. Use the standard deviation of the bootstrap estimates as an estimate of the standard error

Assessing covariate balance with weights

Covariate balance check with standardized differences

  • Covariate balance: can be checked on the weighted sample using standardized difference \[ smd = \frac{\bar{X}_{\text{treatment}} - \bar{X}_{\text{control}}}{\sqrt{\frac{s^2_{\text{treatment}} + s^2_{\text{control}}}{2}}} \]

    • Weighted means \(\bar{X}_{\text{treatment}}\), \(\bar{X}_{\text{control}}\)
    • Weighted variances \(s^2_{\text{treatment}}\), \(s^2_{\text{control}}\)

Balance check tools

  • Table 1

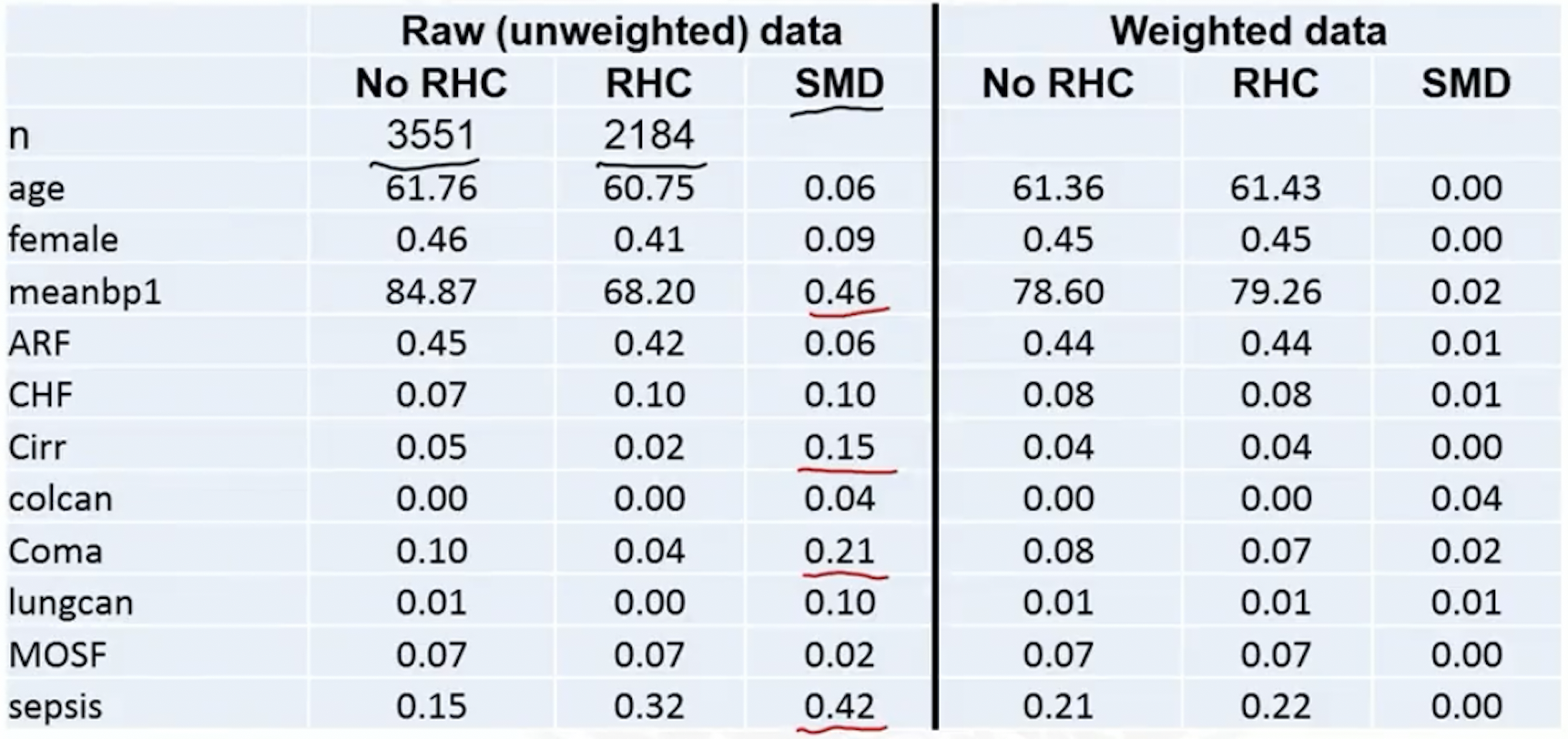
  • SMD plot

If imbalance after weighting

  • Refine propensity score model

    • Interactions
    • Non-linearity

  • Then reaccess balance

Problems and remedies for large weights

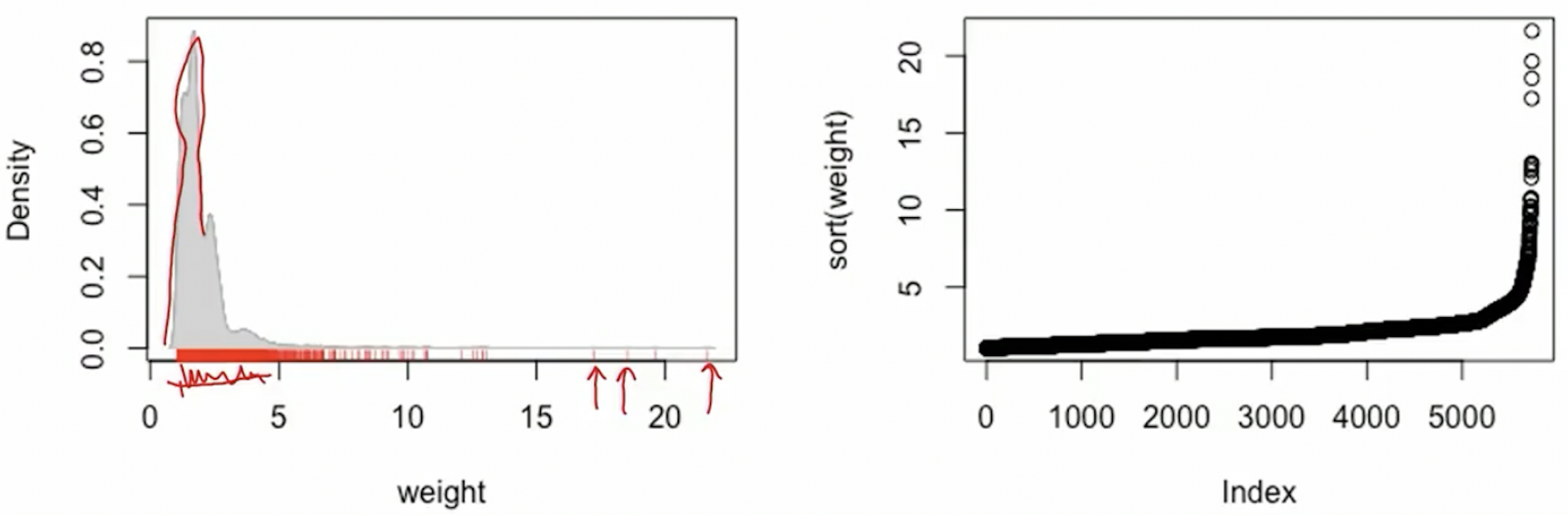
Larger weights lead to more noise

  • For an object with a large weight, its outcome data can greatly affect parameter estimation

  • An object with large weight can also affect standard error estimation, via bootstrap, depending on whether the object is selected or not

  • An extremely large weights means the probability of that treatment is very small, thus a potential violation of the positivity assumption

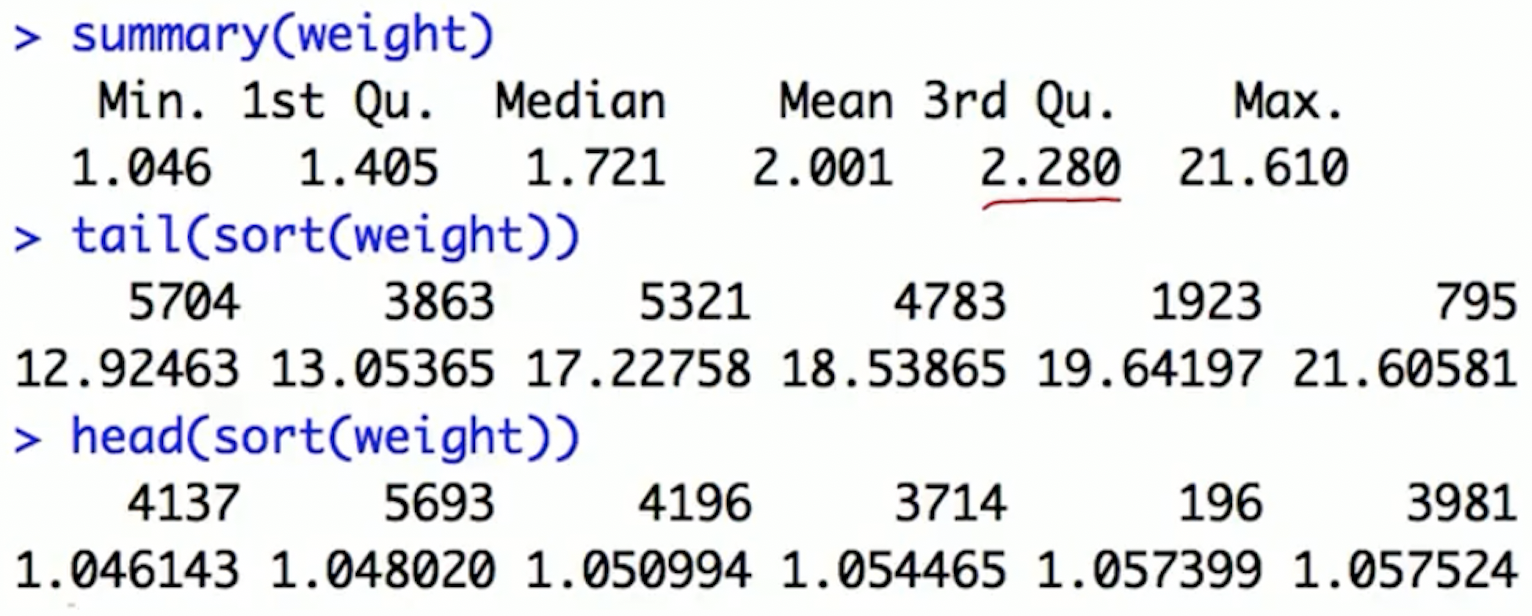
Check weights via plots and summary statistics

  • Investigate very large weights: identify the subjects with large weights and find what’s unusual about them

Option 1: trimming the tails

  • Large weights: occur in the tails of the propensity score distribution

  • Trim the tails to eliminate some extreme weights

    • Remove treated subjects whose propensity scores are above the 98th percentile from the distribution among controls
    • Remove control subjects whose propensity scores are below the 2nd percentile from the distribution among treated

  • Note: trimming the tails changes the population

Option 2: truncating the weights

  • Another option to deal with large weights is truncation

  • Weight truncation steps

    1. Determine a maximum allowable weight
    • Can be a specific value (e.g., 100)
    • Can based on a percentile (e.g., 99th)
    1. If a weight is greater than the maximum allowable, set it to the maximum allowable value
  • Bias-variance trade-off
    • Truncation: bias, but smaller variance
    • No truncation: unbiased, larger variance

  • Truncating extremely large weights can result in estimators with lower MSE

References